In elementary geometry, a polygon is a plane figure that is bounded by a finite chain of straight line segments closing in a loop to form a closed chain or circuit. Or simply a closed plane figure bounded by three or more line segment to form a closed loop is called a polygon.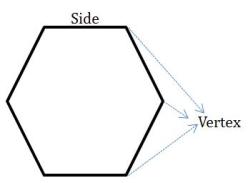
Nomenclature:
- The line segments forming the polygon are called sides.
- The point of intersection of two line segments is called a vertex.
- Number of vertices of a polygon is equal to the number of line segments or sides.
Different types of Polygons: This is based on the number of sides that the polygon has. Here are few examples: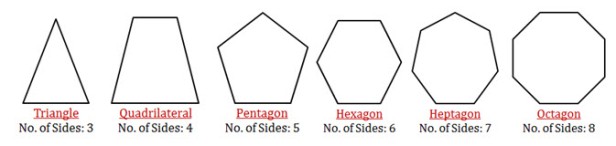
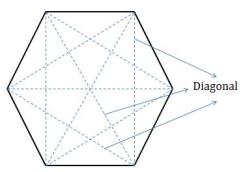 Diagonal of a Polygon: A line segment joining any two non-consecutive vertices is called
Diagonal of a Polygon: A line segment joining any two non-consecutive vertices is called
a diagonal of the polygon.
The dotted lines are diagonals of the shown polygons.
Interior and Exterior Angles of a Polygon: This is an important concept.
are interior angles. These are made by the two sides of the polygon.
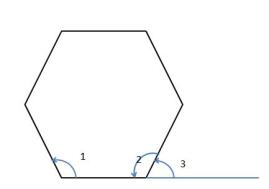
is called an exterior angle. This is formed by extending a side of the polygon as shown in the adjacent figure.
Just by looking at the figure you can tell that
Hence we can say that:
Exterior Angle + Adjacent Interior Angle
Convex Polygon vs Concave Polygon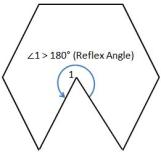
If the interior angle of the polygon is less than , then it is called convex polygon. If you look at any of the polygons shown above, you will see that all the interior angles are less than
.
But there can be cases where the interior angle of a polygon could be more than . Take a look at the adjacent figure. Here you will see that
(which is a reflex angle).
Regular Polygon: A polygon that satisfies the following condition is called a regular polygon.
- All sides are equal
- All interior angles are equal
- All exterior angles are equal
For a regular polygon with sides we have the following:
Proof:
A polygon can be divided into triangles.
See a few examples in the adjacent figure.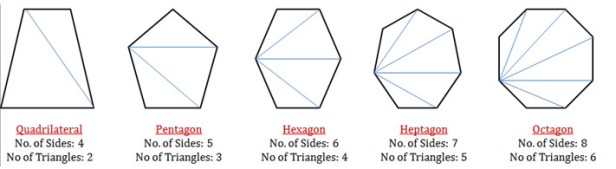
We know that the sum of the angles of a triangle is .
Proof:
From the above point 2, we can also say that
We already know that

Hi
The more intersting thing is not the exterior angels but the center angels where you have their sum of 360 ° .
A single center angel therefor has 360°/n .
same 2×pi/n
How can you count the hole circle in U=2×pi×r in the infinity
If you think of this you construkt a spiral of U=squr of 2 × pi
U (center)=U or U (interior)=U
exterior is trivial if you think of a quader
Good luck