Parallel Linesp1

Two straight lines, in the same plane, are said to be parallel if they do not intersect, no matter on how long they are extended on either sides.

Transversal

A straight line that intersects two or more lines in a plane is called a transversal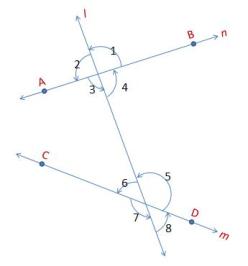p2.

When two lines m and n are intersected by line l, then there are eight angles that are formed as shown in the figure. These angles can be grouped into different groups:

  1. Pairs of Corresponding Angles: (\angle 1,\ \angle 5),\ (\angle 2,\ \angle 6),\ (\angle 3,\ \angle 7),\ (\angle 4,\ \angle 8)
  2. Pairs of Alternate Interior Angles: (\angle 3,\ \angle 5),\ and\ (\angle 4,\ \angle 6)
  3. Pair of Alternate Exterior Angles: (\angle 2,\ \angle 8),\ and\ (\angle 1,\ \angle 7)
  4. Pair of Consecutive Interior Angles: (\angle 4,\ \angle 5),\ and\ (\angle 3,\ \angle 6)

Note:

The opposite angles are equal. Therefore (\angle 1,=\angle 3),\ (\angle 2,=\angle 4),\ (\angle 5,=\angle 7),\ (\angle 6,=\angle 8) . These are vertically opposite angles (please refer to Lecture Notes Part 2).

Properties of Angles Associated with Parallel Lines

Now let’s extend this understanding to a pair of parallel lines that is intersected by another lines. Same logic, just that m and n are parallel lines.

  1. Corresponding Angles are equal: (\angle 1,=\angle 5),\ (\angle 2,=\angle 6),\ (\angle 3,=\angle 7),\ (\angle 4,=\angle 8) 

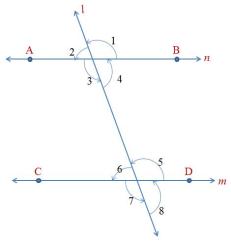  2. p3Alternate Interior Angles are Equal    : (\angle 3,=\angle 5),\ (\angle 4,=\angle 6)
  3. Alternate Exterior Angles are Equal: (\angle 2,=\angle 8),\ (\angle 1,=\angle 7)
  4. Consecutive Interior Angles are supplementary (i.e. the sum of the angles is 180°: (\angle 4+\angle 5=180^{\circ}),\ and\ (\angle 3+\angle 6=180^{\circ})

The converse of the above is also true:

  1. If the Corresponding Angles are equal, then the lines are parallel.
  2. If the alternate angles are equal, then the lines are parallel.
  3. If the consecutive interior angles are supplementary, then the lines are parallel.

Note:

  1. To intersecting lines cannot be both parallel to the same straight lines.
  2. Also, straight lines parallel to the same lines are also parallel to each other.
  3. Through a given point, there can only be one straight line parallel to a given line.