Class 8, Lecture Notes - Quadrilaterals, Quadrilaterals

Class 8: Quadrilaterals (Lecture Notes III)

Date: September 18, 2016Author: ICSE CBSE ISC Board Mathematics Portal for Students 0 Comments

Type of Quadrilaterals…continued

Rectangle

Definition: A parallelogram where all the four angles are right angles is called a rectangle.

Properties: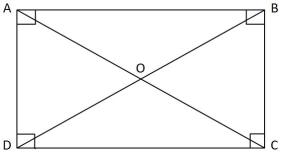

1) Opposite sides are equal and parallel to each other.

$AB \parallel DC \ and \ AB=DC$

$AD \parallel BC \ and \ AD=BC$

2) Each angle measures $90^{\circ} \ i.e.\ \angle A=\angle B=\angle C=\angle D=90^{\circ}$

3) The diagonals are equal i.e. $AC = BC$

4) The diagonals $(AC \ and\ BD)$ bisect each other

$AO = OC$

$DO = OB$

Theorem: The diagonals of a rectangle are equal.

Given: $ABCD$ is a rectangle and the diagonals are $AC \ and\ BD$

To prove: $AC = BD$

Consider $\Delta BCD \ and\ \Delta ACD$

$AD = BC$ (given that it is a rectangle)

$DC$ is common

$\angle ADC =\angle BCD$ (right angles)

Hence $\Delta ACD \cong \Delta BCD$ (S.A.S axiom)

Therefore $AC = BD$ . Hence Proved

Square

A parallelogram which has all sides equal and all four angles are right angle is called a square. Or we can also say that a square is a rectangle that has all four sides equal.

Properties of square:

1) All sides are equal i.e. $AB = BC = CD = DA$

2) Each angle measures $90^{\circ} i.e. \angle A =\angle B =\angle C =\angle D = 90^{\circ}$

3) The diagonals are equal i.e. $AC = BC$

4) The diagonals $(AC \ and\ BD)$ bisect each other $AO = OC\ \& \ DO = OB$

The diagonals intersect at right angles i.e. $AC \perp BD$

Theorem: The diagonals of a square are equal and perpendicular to each other.

To prove: $AC = BD \ and\ AC \perp BD$

Given: Square $ABCD$ , Diagonals $AC \ and\ BD \ intersect \ at \ O$

Proof:

Consider $\Delta BCD \ and\ \Delta ACD$

$AD = BC$ (given that it is a square)

$DC$ is common

$\angle ADC = \angle BCD \$ (right angles)

Hence $\Delta ACD \cong \Delta BCD$ (S.A.S axiom)

Therefore $AC = BD$ . Hence Proved

Consider $\Delta COD \ and\ \Delta AOD$

$OC = OA$ (diagonals of a parallelogram bisect each other)

$DO$ is common

$D=DC$ (Sides of a triangle)

Hence $\Delta COD \cong \Delta AOD$ (S.S.S axiom)

Hence $\angle DOC=\angle DOA$

We know that $\angle DOC+\angle DOA=180^{\circ}$

Therefore $\angle DOC=\angle DOA=90^{\circ}$

Hence $DO\perp AC \ i.e.\ AC\perp BD$

Leave a ReplyCancel reply