Other Solved Mathematics Board Papers
MATHEMATICS (ICSE – Class X Board Paper 2020)
Two and Half Hour. Answers to this Paper must be written on the paper provided separately. You will not be allowed to write during the first 15 minutes. This time is to be spent in reading the question paper.
The time given at the head of this Paper is the time allowed for writing the answers. Attempt all questions form Section A and any four questions from Section B. All working, including rough work, must be clearly shown and must be done on the same sheet as the rest of the Answer. Omission of essential working will result in the loss of marks.
The intended marks for questions or parts of questions are given in brackets [ ].
Mathematical tables are provided.
SECTION A [40 Marks]
(Answer all questions from this Section.)
Question 1:
(a) Solve the following quadratic equation:
Give your answer correct to two decimal places. [3]
(b) Given
If , where
is the identity matrix of Order
, find
and
. [3]
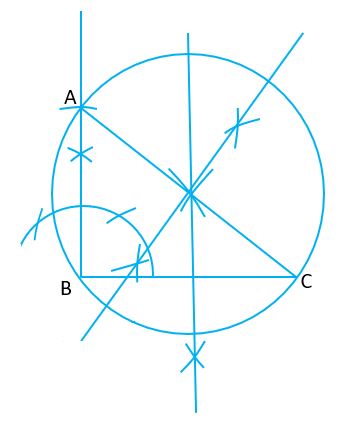
(c) Using ruler and compass construct a triangle where
cm,
cm and
. Hence construct a circle circumscribing the triangle
. Measure and write down the radius of the circle. [4]
Answers:
(a) Given
Comparing it with we get ,
and
We know,
Therefore
or
Hence roots are and
(b) Given: and
Comparing we get
Similarly,
(c)
cm and
cm
Radius of the circle cm
Question 2:
(a) Use factor theorem to factorize completely. [3]
(b) Solve the following in-equation and represent the solution set on the number line.
[3]
(c) Draw a histogram for the given data using graph paper. [4]
| Weekly Wages (in Rs) | No. of People |
| 3000-4000 | 4 |
| 4000-5000 | 9 |
| 5000-6000 | 18 |
| 6000-7000 | 6 |
| 7000-8000 | 7 |
| 8000-9000 | 2 |
| 9000-10000 | 4 |
Answers:
(a) Let
By trial and error, let
Therefore
Hence we can say that is a factor of
Now,
Now factorize
Therefore complete factorization is
(b)
First solve:
Also solve
Hence the solution set

(c)

Question 3:
(a) In the figure given below, is the center of the circle and
is a diameter, if
and
, find [3]
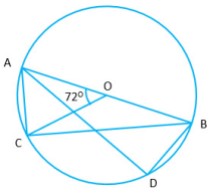
i)
ii)
iii)
(b) Prove that
[3]
(c) In what ratio is the line joining and
is divided by y-axis. Also find the coordinates of the point of intersection. [4]
Answers:
(a)
i) We know, The angle which an arc of a circle subtends at the center is double that which it subtends on any point of the part of the circumference.
Therefore
ii) Given
The chord of the same length subtend the same angle
iii) (semi circular angles are
)
In
(b)
LHS
RHS Hence proved.
(c) 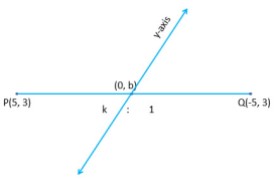 Let the point of intersection be
Let the point of intersection be
Let the ratio of in which the line segment gets divided be
Using section formula
and
Hence the ratio is
Therefore
Therefore the coordinates of the point of intersection is
Question 4:
(a) A solid spherical ball of radius cm is melted and recasted in
identical spherical marbles. Find the radius of each marble. [3]
(b) Each of the letters of the word is written on identical circular discs and put in a bag. They are well shuffled. If a disc is drawn at random from the bag, what is the probability that the letter is
i) a vowel
ii) One of the first letters of the English alphabet which appears in a given word
iii) One of the last letters of the English alphabet which appears in a given word [3]
(c) Mr. Bedi visits the market and buys the following articles:
Medicines costing Rs. , GST @
A pair of shoes costing Rs. , GST @
A laptop bag costing Rs with a discount or
, GST @
i) Calculate the total amount of GST paid
ii) The total bill amount including GST paid by Mr. Bedi [4]
Answers:
(a) Let be the radius of spherical ball and
be the radius of the spherical marble
Volume of spherical ball
Volume of spherical marble
cm
(b) First 9 letters:
Last 9 letters:
Total outcomes
i) No. of vowels
Therefore probability
ii) There are probable outcomes
Therefore probability
iii) There are probable outcomes
Therefore probability
(c)
| Article | Cost ( Rs.) | Final Cost (Rs.) | GST Rate | GST ( Rs.) | Final Price (Rs.) |
| Medicines | 950 | 950 | 5% | 47.50 | 997.50 |
| Shoes | 3000 | 3000 | 18% | 540 | 3540 |
| Laptop Bag | 1000 @ 30% discount | 700 | 18% | 126 | 829 |
| Total (Rs.) | 713.50 | 5363.50 |
Therefore
i) Calculate the total amount of GST paid Rs.
ii) The total bill amount including GST paid by Mr. Bedi Rs.
SECTION B [40 Marks]
(Attempt any four questions from this Section.)
Question 5:
(a) A company with shares of nominal value Rs.
declares and annual dividend of
. Calculate:
i) the total amount of dividend paid by the company
ii) annual income of Mr. Sharma who holds shares of the company.
If the return percent of Mr. Sharma for his shares is , find the market value of each share. [3]
(b) The mean of the following data is . Calculate the value of
. [3]
| Marks | 5 | 10 | 15 | 20 | 25 |
| No. of Students | 3 | 7 | 9 | 6 |
(c) The and the last term of a geometric progression are
and
respectively. If the common ratio is positive, find the first term, common ration and the number of terms of the series. [4]
Answers:
(a) Number of shares
Nominal Value Rs.
Dividend
i) Dividend
Rs.
ii) shares
Dividend
Rs.
Return
Rs.
Therefore Market Value
Rs.
(b)
| Marks |
No. of Students |
|
| 5 | 3 | 15 |
| 10 | 7 | 70 |
| 15 | ||
| 20 | 9 | 180 |
| 25 | 6 | 150 |
Given: Mean
We know
(c) term
term
Last term
We know,
… … … … … i)
Similarly,
… … … … … ii)
Dividing ii) by i) we get
Using i) we get
We know that
Question 6:
(a) If and
. Find:
[3]
(b) 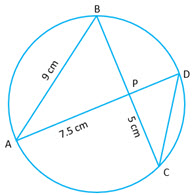 In the given figure
In the given figure cm,
cm and
cm
Chord and
intersect at
.
i) Prove that
ii) Find the length of
iii) Find area of area of
[3]
(c) From the top of a cliff, the angle of depression of the top and bottom of a tower are observed to be and
respectively. If the height of the tower is
m, Find:
i) the height of the cliff
ii) the distance between the cliff and the tower. [4]
Answers:
(a) Given
and
(b)
i) Consider and
( Vertically opposite angles)
(angles subtended by an arc on the circumference are equal)
(By AA similarity criterion)
ii) Since
cm
iii)
c)
In
… … … … … i)
In
… … … … … ii)
Substituting
m
m
i) the height of the cliff m
ii) the distance between the cliff and the tower m
Question 7:
(a) Find the value of is the lines
and
are perpendicular to each other. Hence find the equation of a line passing through
and parallel to
. [3]
(b) Using properties of proportion find given
[3]
(c) 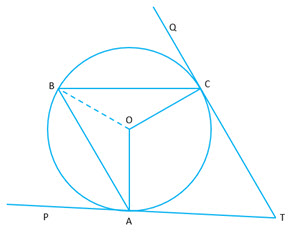 In the given figure,
In the given figure, and
are two tangents to the circle with center
, touching at
and
respectively. If
and
, find:
i) and
ii)
iii) [4]
Answers:
(a) Given
Therefore slope
Similarly,
Therefore slope
We know
Therefore slope
Therefore equation of line
(b)
Applying componendo and dividendo
Applying componendo and dividendo
(c)
i)
Since is an isosceles triangle
Similarly, is an isosceles triangle
ii)
Angle subtended by an arc at the center is twice that subtended on the circumference.
iii) is a quadrilateral. We know that the sum of all the internal angles of a quadrilateral is
Hence,
Question 8:
(a) What must be added to the polynomial , so that it leaves a remainder
when divided by
? [3]
(b) Mr. Sonu has a recurring deposit account and deposits Rs. per month for
years. If he gets Rs.
at the time of maturity, find the rate of interest. [3]
(c) Use a graph paper for this. [4]
Take cm
unit on both x and y axes.
i) Plot the following points on your graph sheet and
ii) Reflect point and
on the x axis and name then
and
respectively.
iii) Join the points and
in order. Name the closed figure formed.
Answers:
(a) Given :
When divided by
(b) Given Rs.
years
months
Rs.
Interest Rs.
Interest
(c)
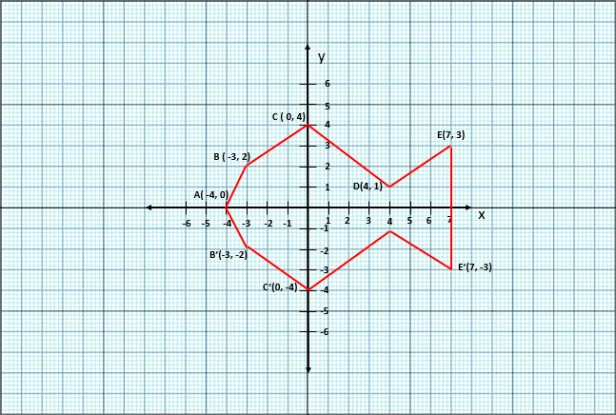
The figure formed is a nonagon (nine edges). It is a FISH.
Question 9:
(a) students enter for a game of shot put competition. The distance thrown ( in meters) is recorded below. [6]
| Distance in m | 12-13 | 13-14 | 14-15 | 15-16 | 16-17 | 17-18 | 18-19 |
| Number of Students | 3 | 9 | 12 | 9 | 4 | 2 | 1 |
Use a graph paper to draw an ogive for the above distribution.
Use a scale of cm
m on x-axis and
cm
students on the other axis.
Hence using your graph paper find:
i) the median
ii) Upper Quartile
iii) Number of students who cover a distance which is above
m
(b) If
, prove that
[4]
Answers:
(a)
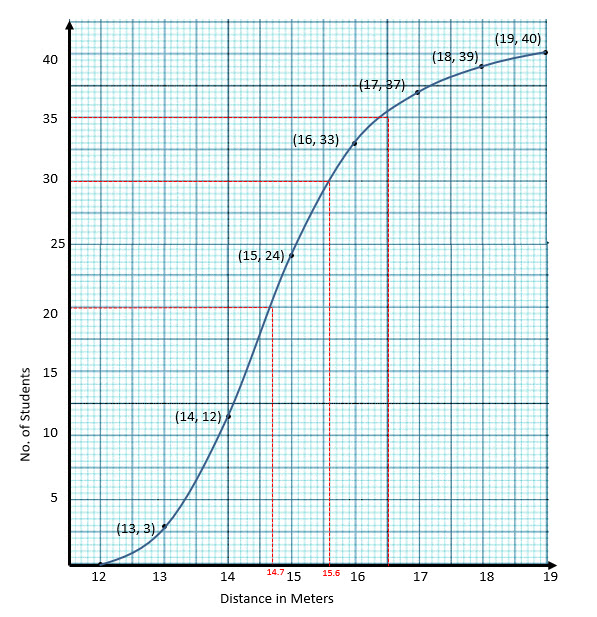
i) the median
ii) Upper Quartile
iii) Number of students who cover a distance which is above
m
students
(b)
Applying componendo and dividendo
Squaring both sides
Applying componendo and dividendo
. Hence proved.
Question 10:
(a) If the terms of an AP is equal to four time its first term and the sum of first six terms is
, find the first term and the common difference. [3]
(b) The difference of two natural numbers us and their product is
. Find the numbers. [3]
(c) Use ruler and compass for this question. Construct a circle of radius cm. Draw a chord
cm.
i) Find the locus of points equidistant from and
. Mark the point where it meets the circle as
.
ii) Join and find the locus of points which are equidistant from
and
. mark the point where it meets the circle as
.
Join and
. Measure and write down the length of side
of quadrilateral
. [4]
Answers:
(a) and
We know that
… … … … … i)
Also
… … … … … ii)
Solving i) and ii)
Substituting in i)
Therefore first term and common difference
(b) Let the two natural numbers be and
Therefore
Also
Substituting
( not a natural number).
Therefore . Substituting we get
(c) 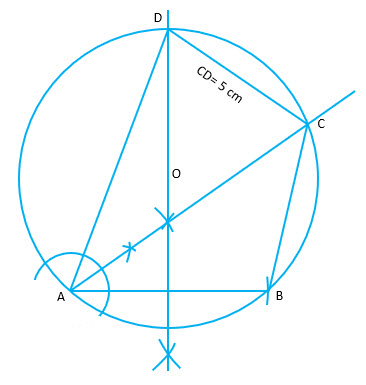
Step 1:Draw a circle of radius 3.5 cm.
Step 2: Then take a point A and draw an arc 6 cm long to intersect the circle at B. Join AB. That is the chord
Step 3: Locus of equidistant points for AB is the perpendicular bisector. Draw perpendicular bisector.
Step 4: Mark point D. Join AD.
Step 5: Draw an angle bisector of angle DAB. This is the locus for equidistant point for point on line AD and AB.
Step 6: Measure CD.
Question 11:
(a) A model of a high rise building is made to a scale of .
i) if the height of the model is m, find the height of the actual building.
ii) If the floor area of a flat in the building is , find the floor are of that in the model.
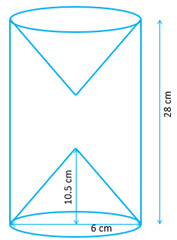
(b) From a solid wooden cylinder of height cm and diameter
cm. Two conical cavities are hollowed out. The diameters of the cone is also
cm and height is
cm.
Taking
, find the volume of the remaining solid.
(c) Prove the identity:
Answers:
(a) Scale
m
i)
m
ii)
or
(b) Volume of a cylinder 
Volume of a cone
Given : cm
cm
cm
Volume of cylinder
Volume of cones
Therefore Volume of remaining solid
(c) LHS
RHS. Hence proved.
