Class 8: Fractions – Lecture Notes – ICSE / ISC / CBSE Mathematics Portal for K12 Students

Fractions:

The number of the form $(a/b)$ , where $a$ and $b$ are natural numbers are known as fractions. In a fraction $(a/b), a$ is known as numerator and $b$ is known as denominator. Note:

Fraction is a part of whole.
The numerator and denominator of a fraction are called its terms.

$\displaystyle \text{ Example:} \frac{7}{10} \text{ is a fraction where the numerator is 7 and the denominator is 10}$

Types of Fractions:

Decimal Fractions: A fraction whose denominator is any of the numbers $10, 100, 1000$ etc., is called a decimal fraction.

$\displaystyle \text{ Example: } \frac{7}{10} , \frac{71}{100} , \frac{77}{100} \text{ etc. are all decimal fractions}$

Vulgar Fraction: A fraction whose denominator is a natural number other than the numbers $10, 100, 1000$ , etc., is called a Vulgar Fraction.

$\displaystyle \text{ Example: } \frac{7}{9} , \frac{71}{87} , \frac{77}{876} \text{ etc. are all Vulgar fractions}$

Proper Fraction: A fraction whose numerator is less than its denominator is called proper fractions.

$\displaystyle \text{ Example: } \frac{7}{19} , \frac{71}{827} , \frac{771}{876} \text{ etc. are all Proper fractions}$

Improper Fraction: A fraction whose numerator is greater than or equal to its denominator, is called an improper fraction.

$\displaystyle \text{ Example: } \frac{71}{19} , \frac{1171}{827} , \frac{2771}{876} \text{ etc. are all Improper fractions}$

Mixed Number (or Mixed Fraction): When an improper fraction is written as a combination of whole number and a proper fraction, it is called a mixed number (or mixed fraction).

$\displaystyle \text{ Example: } 2\frac{7}{3} , 3\frac{71}{100} , 4\frac{77}{1000} \text{ etc. are all Mixed Numbers ( or Mixed Fractions) }$

How to Convert a Mixed Fraction into an Improper Fraction?

The numerator is obtained by multiplying the whole number part with the denominator of the fractional part and then adding the numerator of the fractional part to the product. The denominator of the fractional part forms the denominator of the improper fraction.

$\displaystyle \text{ Example: } 9\frac{2}{3} = \frac{9 \times 3 + 2}{3} = \frac{29}{3}$

How to convert an improper fraction into a Mixed Fraction?

Divide the numerator of the given improper fraction by the denominator. The quotient obtained forms the whole number part, the remainder obtained forms the numerator of the fractional part and the divisor forms the denominator of the fractional part.

$\displaystyle \text{ Example: } \frac{29}{3} = 9\frac{2}{3}$

Simple Fraction: A fraction each of whose term is a whole numbers is called a simple fraction.

$\displaystyle \text{ Example: } \frac{2}{3} , \frac{9}{5} , \frac{7}{70} \text{ etc. are all simple fractions}$

Complex Fraction: A fraction at least one of whose terms is itself a fraction is called a complex fraction.

$\displaystyle \text{ Example: } \frac{2}{(\frac{3}{4})} , \frac{(\frac{9}{23})}{5} , \frac{7}{(\frac{70}{87})} \text{ etc. are all scomplex fractions}$

Equivalent Fractions: Fractions having the same value are called equivalent fractions.

$\displaystyle \text{ Example: } \frac{2}{3} , \frac{4}{6} , \frac{10}{20} \text{ etc. are all equivalent fractions}$

Like Fractions: Fractions having the same denominators are called like fractions.

$\displaystyle \text{ Example: } \frac{2}{9} , \frac{3}{9} , \frac{5}{9} \text{ etc. are all decimal fractions}$

Unlike Fractions: Fractions having different denominators are called unlike fractions.

$\displaystyle \text{ Example: } \frac{2}{9} , \frac{3}{19} , \frac{5}{29} \text{ etc. are all Unlike fractions}$

How to convert Unlike Fractions into Like Fractions?

Find the L.C.M of the denominators of all the given unlike Fractions.
Convert each of the fractions into an equivalent fraction having denominator equal to the L.C.M of the denominator.
All the fractions would have the same denominator now and would be like fractions.

$\displaystyle \text{ Example: Convert the fractions } \frac{3}{8} , \frac{11}{12} , \frac{8}{15} \text{ etc. into like fractions}$

$\displaystyle \text{ LCM }= 2 \times 2 \times 3 \times 2 \times \times 5$

$\displaystyle \text{ Now convert the fractions to 120 denominator}$

$\displaystyle \frac{3}{8} = \frac{3 \times 15}{120} = \frac{45}{120}$

$\displaystyle \frac{11}{12} = \frac{11 \times 10}{120} = \frac{110}{120}$

$\displaystyle \frac{8}{15} = \frac{8 \times 8}{120} = \frac{64}{120}$

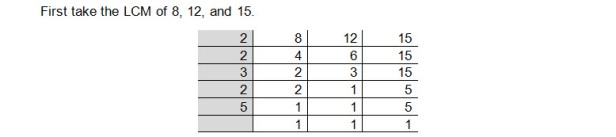
Fractions in Lowest Terms or in Simplest Form

A fraction is said to be in lowest or simplest form if the H.C.F of the numerator and denominator is 1.

The fraction can be reduced to its lowest form if you divide both the numerator and the denominator by their H.C.F.

$\displaystyle \text{ Example: Reduce } \frac{126}{162} \text{ to its lowest form.}$

$\displaystyle \text{ H.C.F of 126 and 162 = 18}$

$\displaystyle \text{ Therefore } \frac{126}{162} = \frac{126 \div 18}{162 \div 18} = \frac{7}{9}$

Comparison of Fractions

Comparison of Fractions with Like Denominators and Unlike Numerators: If the fraction has the same denominator, then the fraction with a larger numerator is the larger fraction.

$\displaystyle \text{ Example: } \frac{5}{7} > \frac{3}{7}$

Comparison of Fractions with Like Numerators by unlike Denominator: If the two fractions have the same numerator but different Denominator, then the fraction with the smaller denominator is the larger fraction.

$\displaystyle \text{ Example: } \frac{7}{24} > \frac{7}{36}$

Comparison of Fractions with Unlike Numerators and Unlike Denominators

Method 1

1. Step 1: First take the LCM of the denominators of the fractions
2. Step 2: Then convert the given unlike fractions into equivalent fractions with the LCM as the common denominator
3. You can compare the like fractions so obtained

$\displaystyle \text{ Example: Arrange the fractions } \frac{5}{9} , \frac{11}{18}, \frac{13}{24} , \text{ and } \frac{17}{36} \text{ in an ascending order}$

$\displaystyle \text{ L.C.F of 9, 8 , 24 and 36 is 72}$

$\displaystyle \text{ Hence we can write } \frac{5}{9} , \frac{11}{18}, \frac{13}{24} , \text{ and } \frac{17}{36} \text{ as } \frac{40}{72} , \frac{44}{72}, \frac{39}{72} , \text{ and } \frac{34}{72}$

$\displaystyle \text{ Hence the ascending order is } \frac{34}{72} , \frac{39}{72}, \frac{40}{72} , \text{ and } \frac{44}{72}$

Method 2

1. Short Cut Method (Cross Multiplication Method)
2. If are two fractions to be compared then

$\displaystyle \text{ i) } \frac{a}{b} > \frac{c}{d} \text{ if } ad > bc$

$\displaystyle \text{ ii) } \frac{a}{b} = \frac{c}{d} \text{ if } ad = bc$

$\displaystyle \text{ iii) } \frac{a}{b} < \frac{c}{d} \text{ if } ad < bc$

To Insert Fractions between Fractions

$\displaystyle \text{ If } \frac{a}{b} \text{ and } \frac{c}{d} \text{ are two fractions, then If } \frac{a+c}{b+d} \text{ lies between } \frac{a}{b} \text{ and } \frac{c}{d}$

Example:

$\displaystyle \text{ If } \frac{5}{6} \text{ and } \frac{7}{8} \text{ are two fractions, then If } \frac{5+7}{6+8} = \frac{6}{7} \text{ lies between } \frac{5}{6} \text{ and } \frac{7}{8}$

Operations on Fractions

Addition of Fractions

Addition of Like Fractions

$\displaystyle \text{ Sum of like Fractions } = \frac{\text{ Sum of the Numerators } }{ \text{ Common Dinominators } }$

2. Addition of unlike Fractions

1. 1. Step 1: Find the LCM of Denominators of unlike fractions
  2. Step 2: Convert unlike fractions into equivalent Fractions with their LCM as the common Denominators
  3. Step 3: Add the like fractions so obtained

$\displaystyle \text{ Example:} \\ \\ \text{ Add} \frac{5}{6} \text{ and } \frac{7}{8} .\text{ LCM of 6 and 8 is 24 . So } \frac{5}{6} \text{ and } \frac{7}{8} \text{ can be written as } \frac{20}{24} \text{ and } \frac{21}{24}$

$\displaystyle \text{ Therefore the sum of } \frac{5}{6} + \frac{7}{8} = \frac{20}{24} + \frac{21}{24} = \frac{41}{24}$

Subtraction of Fractions

The same rules are followed as above. Instead of + operator, – operator comes into play.

$\displaystyle \text{ Example:} \\ \\ \text{ Subtract} \frac{5}{6} \text{ from} \frac{7}{8} .\text{ LCM of 6 and 8 is 24 . So } \frac{5}{6} \text{ and } \frac{7}{8} \text{ can be written as } \frac{20}{24} \text{ and } \frac{21}{24}$

$\displaystyle \text{ Therefore the subtraction of } \frac{5}{6} - \frac{7}{8} = \frac{20}{24} - \frac{21}{24} = \frac{-1}{24}$

Multiplication of Fractions

$\displaystyle \text{ Product of like Fractions } = \frac{\text{ Product of the Numerators } }{ \text{ Product of Dinominators } }$

The answer obtained is reduced to the lowest form by dividing the numerator and denominator by their HCF.

An easier way of multiplying fractions is that if there are common factors in one of the numerators and one of the denominators, then we can cancel that before multiplying.

$\displaystyle \text{ Example: Multiply } \frac{3}{14} \times \frac{7}{18} = \frac{3 \times 7}{14 \times 18} = \frac{1}{12}$

Division of Fractions

In order to divide two fractions, we just multiply the dividend by the reciprocal of the Divisor.

Reciprocal of a Non-Zero Fraction

Let $(a/b)$ be a non-zero fraction. Then $a$ and $b$ are natural numbers.

The Fraction $(b/a)$ is called the reciprocal of $(a/b)$

Simplification of Expressions Involving Fractions

Use of BODMAS Rule (remember the word BODMAS)

We simplify the expressions by applying the operations strictly in the order
1. Brackets
2. Of
3. Division
4. Multiplication
5. Addition
6. Subtraction
Removal of Brackets: Follow this order
1. Bar or Vinculum (—)
2. Parenthesis ( )
3. Curly Brackets { }
4. Square Brackets [ ]

Example 1: Simplify the following:

$\displaystyle 7\frac{1}{2} + \frac{1}{2} \div \frac{1}{2} \text{ of } \frac{1}{4} - \frac{2}{5} \times 2\frac{1}{3} \div 1\frac{7}{8} \text{ of } ( 1\frac{2}{5} - 1\frac{1}{3} )$

$\displaystyle = \frac{15}{2} + \frac{1}{2} \div \frac{1}{2} \text{ of } \frac{1}{4} - \frac{2}{5} \times \frac{7}{3} \div \frac{15}{8} \text{ of } ( \frac{7}{5} - \frac{4}{3} )$

$\displaystyle = \frac{15}{2} + \frac{1}{2} \div \frac{1}{2} \text{ of } \frac{1}{4} - \frac{2}{5} \times \frac{7}{3} \div \frac{15}{8} \text{ of } ( \frac{21-20}{5} )$

$\displaystyle = \frac{15}{2} + \frac{1}{2} \div \frac{1}{2} \text{ of } \frac{1}{4} - \frac{2}{5} \times \frac{7}{3} \div \frac{15}{8} \text{ of } ( \frac{1}{5} )$

$\displaystyle = \frac{15}{2} + \frac{1}{2} \div \frac{1}{8} - \frac{2}{5} \times \frac{7}{3} \div \frac{1}{8}$

$\displaystyle = \frac{15}{2} + \frac{1}{2} \times\frac{8}{1} - \frac{2}{5} \times \frac{7}{3} \times \frac{8}{1}$

$\displaystyle =\frac{15}{2} + 4 - \frac{112}{15}$

$\displaystyle = \frac{225-120-224}{30}$

$\displaystyle =\frac{121}{30}$

$\displaystyle = 4\frac{1}{30}$

Example 2: Simplify the following:

$\displaystyle \Big[ 3\frac{1}{4} \div \Big\{ 1\frac{1}{4} - \frac{1}{2} \Big( 2\frac{1}{2} - \Big( \frac{1}{4} - \frac{1}{6} \Big) \Big) \Big\} \Big]$

$\displaystyle = \Big[ \frac{13}{4} \div \Big\{ \frac{5}{4} - \frac{1}{2} \Big( \frac{5}{2} - \Big( \frac{1}{4} - \frac{1}{6} \Big) \Big) \Big\} \Big]$