\displaystyle \textbf{Basic Geometrical Concepts}

\displaystyle \textbf{Axioms}

\displaystyle \text{An axiom is a basic statement that is accepted as true without proof.}
\displaystyle \text{Axioms provide the starting point for mathematical reasoning and are used}
\displaystyle \text{to establish other mathematical results.}

\displaystyle \text{Examples:}

\displaystyle \text{The halves of equal quantities are equal.}

\displaystyle \text{The whole is greater than the part.}

\displaystyle \text{Things which are equal to the same thing are equal to one another.}

\displaystyle \textbf{Statement}

\displaystyle \text{A statement or proposition is a declarative sentence that is either true}
\displaystyle \text{or false, but not both.}

\displaystyle \text{Examples:}

\displaystyle \text{``5 is an odd integer'' is a true mathematical statement.}

\displaystyle \text{``5 is an even integer'' is a false mathematical statement.}

\displaystyle \text{``11 is a cool number'' is not a mathematical statement because the word}
\displaystyle \text{``cool'' is subjective and has no definite mathematical truth value.}

\displaystyle \text{In Euclidean geometry, the sum of the interior angles of a triangle is}
\displaystyle 180^\circ.

\displaystyle \textbf{Theorem}

\displaystyle \text{A theorem is a mathematical statement whose truth has been established}
\displaystyle \text{by proof using definitions, axioms and previously proved results.}

\displaystyle \text{Unlike an axiom, which is accepted without proof, a theorem must be proved.}

\displaystyle \text{Example: Pythagoras' Theorem states that in a right-angled triangle, the}
\displaystyle \text{square of the hypotenuse is equal to the sum of the squares of the other}
\displaystyle \text{two sides. Thus, if }c\text{ is the hypotenuse, then}

\displaystyle a^2+b^2=c^2.

\displaystyle \textbf{Fundamental Geometrical Terms}

\displaystyle \textbf{Point}

\displaystyle \text{A point represents an exact position or location in a plane or in space.}
\displaystyle \text{It has no length, breadth or thickness and hence has no dimensions.}

\displaystyle \text{A point is represented by a small dot and is usually named by a capital}
\displaystyle \text{letter such as }A,\ B,\ C,\text{ etc.}

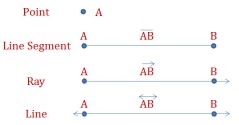
\displaystyle \textbf{Line Segment}

\displaystyle \text{A line segment is a part of a line bounded by two distinct endpoints.}
\displaystyle \text{It contains the two endpoints and all the points lying between them.}

\displaystyle \text{A line segment with endpoints }A\text{ and }B\text{ is denoted by}

\displaystyle \overline{AB}.

\displaystyle \text{A line segment has two endpoints and a definite length.} l1

\displaystyle \text{The length of the line segment }\overline{AB}\text{ is denoted by }AB.

\displaystyle \textbf{Ray}

\displaystyle \text{A ray is a part of a line that begins at a fixed point and extends endlessly}
\displaystyle \text{in one direction.}

\displaystyle \text{A ray beginning at }A\text{ and passing through }B\text{ is denoted by}

\displaystyle \overrightarrow{AB}.

\displaystyle \text{The point }A\text{ is called the endpoint or initial point of the ray.}

\displaystyle \text{A ray has one endpoint and does not have a definite length.}

\displaystyle \text{The order of the letters is important. In general,}

\displaystyle \overrightarrow{AB}\ne\overrightarrow{BA}.

\displaystyle \textbf{Line}

\displaystyle \text{A line is a straight path that extends endlessly in both directions.}
\displaystyle \text{It has no endpoints and does not have a definite length.}

\displaystyle \text{A line passing through two distinct points }A\text{ and }B\text{ is denoted by}

\displaystyle \overleftrightarrow{AB}.

\displaystyle \text{A line may also be represented by a lowercase letter such as }l,\ m,\text{ or }n.

\displaystyle \text{The order of the points does not matter when naming a line. Thus,}

\displaystyle \overleftrightarrow{AB}=\overleftrightarrow{BA}.

\displaystyle \textbf{Incidence Axioms on Lines}

\displaystyle \text{The following basic properties describe the relationship between points}
\displaystyle \text{and lines in Euclidean geometry:}

\displaystyle \text{(i) A line contains infinitely many points.}

\displaystyle \text{(ii) Infinitely many lines can be drawn through a given point.}

\displaystyle \text{(iii) Through any two distinct points }A\text{ and }B,\text{ exactly one line}
\displaystyle \text{can be drawn.}

\displaystyle \text{Thus, two distinct points uniquely determine a line.}

\displaystyle \textbf{Collinear Points}

\displaystyle \text{Three or more points are said to be collinear if they lie on the same}
\displaystyle \text{straight line.}

\displaystyle \text{For example, if points }A,\ B\text{ and }C\text{ lie on the same line, then}
\displaystyle A,\ B\text{ and }C\text{ are collinear points.}

\displaystyle \text{Points that do not all lie on the same line are called non-collinear points.}

\displaystyle \textbf{Plane}

\displaystyle \text{A plane is a flat two-dimensional surface that extends endlessly in all}
\displaystyle \text{directions within the plane.} l2

\displaystyle \text{A plane has length and breadth but no thickness.}

\displaystyle \text{Three non-collinear points determine exactly one plane.}

\displaystyle \textbf{Intersecting Lines}

\displaystyle \text{Two distinct lines in a plane that have a common point are called}
\displaystyle \text{intersecting lines.}

\displaystyle \text{The common point is called the point of intersection.}

\displaystyle \text{Two distinct lines can intersect at only one point.}

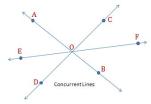\displaystyle \textbf{Concurrent Lines} l3

\displaystyle \text{Three or more lines are said to be concurrent if they all pass through}
\displaystyle \text{the same point.}

\displaystyle \text{The common point is called the point of concurrence.}

\displaystyle \text{For example, the three medians of a triangle are concurrent at a point}
\displaystyle \text{called the centroid.}

\displaystyle \textbf{Parallel Lines} l4

\displaystyle \text{Two distinct lines lying in the same plane are said to be parallel if they}
\displaystyle \text{do not intersect, however far they are extended.}

\displaystyle \text{If lines }l\text{ and }m\text{ are parallel, we write}

\displaystyle l\parallel m.

\displaystyle \text{Parallel lines are always coplanar and have no point in common.}

\displaystyle \textbf{Angles} l8

\displaystyle \text{An angle is a figure formed by two rays having a common endpoint.}
\displaystyle \text{The two rays are called the arms or sides of the angle, and their common}
\displaystyle \text{endpoint is called the vertex of the angle.}

\displaystyle \text{For example, the rays }\overrightarrow{OA}\text{ and }\overrightarrow{OB}
\displaystyle \text{having the common endpoint }O\text{ form the angle }AOB.

\displaystyle \text{It is written as }\angle AOB.

\displaystyle \overrightarrow{OA}\text{ and }\overrightarrow{OB}\text{ are the arms of the angle,}
\displaystyle \text{and }O\text{ is its vertex.}

\displaystyle \text{While naming an angle using three letters, the vertex is always written}
\displaystyle \text{as the middle letter.}

\displaystyle \textbf{Measure of an Angle} l9

\displaystyle \text{The measure of an angle indicates the amount of rotation from one arm of}
\displaystyle \text{the angle to the other arm about their common vertex.}

\displaystyle \text{Angles are commonly measured in degrees, denoted by }{}^\circ.

\displaystyle \text{One complete rotation about a point measures }360^\circ.

\displaystyle \text{Half a complete rotation measures }180^\circ\text{ and a quarter rotation}
\displaystyle \text{measures }90^\circ.

\displaystyle \textbf{Degrees, Minutes and Seconds}

\displaystyle \text{A degree can be divided into smaller units called minutes and seconds.}

\displaystyle 1^\circ=60'\quad\text{and}\quad1'=60''.

\displaystyle \therefore 1^\circ=60\times60''=3600''.

\displaystyle \text{Here, }'\text{ denotes a minute and }''\text{ denotes a second of angular measure.}

\displaystyle \textbf{Measuring and Drawing Angles}

\displaystyle \text{The instrument commonly used to measure and draw angles is called a}
\displaystyle \text{protractor.}

\displaystyle \text{A standard semicircular protractor measures angles from }0^\circ\text{ to }180^\circ.

Kinds of Angles

Name of the Angle Description Diagram
Acute Angle An angle whose measure is more than 0^{\circ}  but less than 90^{\circ}  is called an acute angle. l10
Right Angle An angle whose measure is equal to 90^{\circ}  is called a right angle. l11
Obtuse Angle An angle whose measure is more than 90^{\circ}  but less than 180^{\circ}  is called an obtuse angle. l12
Straight Angle An angle whose measure is equal to 180^{\circ}  is called a straight angle. l13
Reflex Angle An angle whose measure is more than 180^{\circ}  but less than 360^{\circ}  is called a reflex angle. l14
Complete Angle An angle whose measure is equal to 360^{\circ}  is called a complete angle. l15

\displaystyle \textbf{Equal Angles}

\displaystyle \text{Two angles are said to be equal if they have the same measure.}

\displaystyle \text{For example, if }m\angle AOB=40^\circ\text{ and }m\angle PQR=40^\circ,\text{ then}

\displaystyle \angle AOB=\angle PQR.

\displaystyle \textbf{Bisector of an Angle} l16

\displaystyle \text{The bisector of an angle is a ray that divides the angle into two equal angles.}

\displaystyle \text{If }\overrightarrow{OC}\text{ bisects }\angle AOB,\text{ then}

\displaystyle \angle AOC=\angle COB.

\displaystyle \text{Hence,}

\displaystyle m\angle AOC=m\angle COB=\frac{1}{2}m\angle AOB.

\displaystyle \textbf{Complementary Angles}

\displaystyle \text{Two angles are called complementary angles if the sum of their measures}
\displaystyle \text{is }90^\circ.

\displaystyle \text{Thus, if }\angle A\text{ and }\angle B\text{ are complementary, then}

\displaystyle m\angle A+m\angle B=90^\circ.

\displaystyle \text{Each angle is called the complement of the other.}

\displaystyle \text{For example, }35^\circ\text{ and }55^\circ\text{ are complementary angles}
\displaystyle \text{because }35^\circ+55^\circ=90^\circ.

\displaystyle \text{Complementary angles need not be adjacent.}

\displaystyle \textbf{Supplementary Angles}

\displaystyle \text{Two angles are called supplementary angles if the sum of their measures}
\displaystyle \text{is }180^\circ.

\displaystyle \text{Thus, if }\angle A\text{ and }\angle B\text{ are supplementary, then}

\displaystyle m\angle A+m\angle B=180^\circ.

\displaystyle \text{Each angle is called the supplement of the other.}

\displaystyle \text{For example, }70^\circ\text{ and }110^\circ\text{ are supplementary angles}
\displaystyle \text{because }70^\circ+110^\circ=180^\circ.

\displaystyle \text{Supplementary angles need not be adjacent.}

\displaystyle \textbf{Adjacent Angles} l17

\displaystyle \text{Two angles are called adjacent angles if they have a common vertex and a}
\displaystyle \text{common arm, and their interiors do not overlap.}

\displaystyle \text{For example, }\angle AOC\text{ and }\angle COB\text{ are adjacent angles if}
\displaystyle O\text{ is their common vertex and }\overrightarrow{OC}\text{ is their common arm.}

\displaystyle \text{The other arms }\overrightarrow{OA}\text{ and }\overrightarrow{OB}\text{ lie on}
\displaystyle \text{opposite sides of the common arm }\overrightarrow{OC}.

\displaystyle \textbf{Linear Pair of Angles} l18

\displaystyle \text{Two adjacent angles form a linear pair if their non-common arms are}
\displaystyle \text{opposite rays and therefore form a straight line.}

\displaystyle \text{For example, if }\overrightarrow{OA}\text{ and }\overrightarrow{OB}\text{ are}
\displaystyle \text{opposite rays, then }\angle AOC\text{ and }\angle COB\text{ form a linear pair.}

\displaystyle \therefore m\angle AOC+m\angle COB=180^\circ.

\displaystyle \text{Hence, the angles forming a linear pair are always supplementary.}

\displaystyle \text{However, two supplementary angles need not form a linear pair because}
\displaystyle \text{they need not be adjacent.}

\displaystyle \textbf{Vertically Opposite Angles}

\displaystyle \text{When two straight lines intersect, two pairs of vertically opposite angles}
\displaystyle \text{are formed. Each pair of vertically opposite angles is equal.}

\displaystyle \text{Suppose the straight lines }AB\text{ and }CD\text{ intersect at point }O.

\displaystyle \text{The two pairs of vertically opposite angles are:}

\displaystyle \angle AOD\text{ and }\angle BOC,

\displaystyle \angle AOC\text{ and }\angle BOD.

\displaystyle \text{Therefore,}

\displaystyle \angle AOD=\angle BOC\quad\text{and}\quad \angle AOC=\angle BOD.

\displaystyle \textbf{Proof of Vertically Opposite Angles} l19

\displaystyle \text{Given: Lines }AB\text{ and }CD\text{ intersect at point }O.

\displaystyle \text{To prove:}

\displaystyle \text{(i) }\angle BOC=\angle AOD

\displaystyle \text{(ii) }\angle AOC=\angle BOD

\displaystyle \text{Proof:}

\displaystyle \text{Since }\overrightarrow{OC}\text{ stands on the straight line }AB,

\displaystyle \angle AOC+\angle BOC=180^\circ. \qquad\text{[Linear Pair]}

\displaystyle \text{Since }\overrightarrow{OA}\text{ stands on the straight line }CD,

\displaystyle \angle AOC+\angle AOD=180^\circ. \qquad\text{[Linear Pair]}

\displaystyle \therefore \angle AOC+\angle BOC=\angle AOC+\angle AOD.

\displaystyle \therefore \angle BOC=\angle AOD.

\displaystyle \text{Hence, the first pair of vertically opposite angles is equal.}

\displaystyle \text{Similarly, }\overrightarrow{OD}\text{ stands on the straight line }AB.

\displaystyle \angle AOD+\angle BOD=180^\circ. \qquad\text{[Linear Pair]}

\displaystyle \text{Also, }\overrightarrow{OA}\text{ stands on the straight line }CD.

\displaystyle \angle AOD+\angle AOC=180^\circ. \qquad\text{[Linear Pair]}

\displaystyle \therefore \angle AOD+\angle BOD=\angle AOD+\angle AOC.

\displaystyle \therefore \angle BOD=\angle AOC.

\displaystyle \text{Hence, vertically opposite angles are equal.}

\displaystyle \textbf{Perpendicular Lines}

\displaystyle \text{Two lines are said to be perpendicular if they intersect at a right angle.}

\displaystyle \text{If the lines }AB\text{ and }CD\text{ are perpendicular, we write}

\displaystyle AB\perp CD.

\displaystyle \text{The four angles formed by two perpendicular lines are each equal to }90^\circ.

\displaystyle \textbf{Parallel Lines} p1

\displaystyle \text{Two distinct straight lines lying in the same plane are said to be parallel}
\displaystyle \text{if they do not intersect, however far they are extended in either direction.}

\displaystyle \text{If lines }m\text{ and }n\text{ are parallel, we write}

\displaystyle m\parallel n.

\displaystyle \textbf{Transversal} p2

\displaystyle \text{A straight line that intersects two or more lines at distinct points is called}
\displaystyle \text{a transversal of those lines.}

\displaystyle \text{Suppose two lines }m\text{ and }n\text{ are intersected by a transversal }l.

\displaystyle \text{Eight angles are formed at the two points of intersection. These angles can}
\displaystyle \text{be grouped into the following pairs:}

\displaystyle \text{(i) Corresponding Angles:}

\displaystyle (\angle1,\angle5),\quad(\angle2,\angle6),\quad (\angle3,\angle7),\quad(\angle4,\angle8).

\displaystyle \text{(ii) Alternate Interior Angles:}

\displaystyle (\angle3,\angle5)\quad\text{and}\quad(\angle4,\angle6).

\displaystyle \text{(iii) Alternate Exterior Angles:}

\displaystyle (\angle2,\angle8)\quad\text{and}\quad(\angle1,\angle7).

\displaystyle \text{(iv) Consecutive Interior Angles:}

\displaystyle (\angle4,\angle5)\quad\text{and}\quad(\angle3,\angle6).

\displaystyle \text{Consecutive interior angles are also called co-interior angles.}

\displaystyle \textbf{Vertically Opposite Angles Formed by a Transversal}

\displaystyle \text{At each point where the transversal intersects a line, vertically opposite}
\displaystyle \text{angles are formed and are equal. Thus,}

\displaystyle \angle1=\angle3,\qquad\angle2=\angle4,

\displaystyle \angle5=\angle7,\qquad\angle6=\angle8.

$latex \displaystyle \textbf{Properties of Angles Associated with Parallel Lines}p3
&fg=0000ff&s=0$

\displaystyle \text{Suppose the parallel lines }m\text{ and }n\text{ are intersected by a}
\displaystyle \text{transversal }l,\text{ so that }m\parallel n.

\displaystyle \textbf{1. Corresponding Angles are Equal}

\displaystyle \angle1=\angle5,\qquad\angle2=\angle6,

\displaystyle \angle3=\angle7,\qquad\angle4=\angle8.

\displaystyle \textbf{2. Alternate Interior Angles are Equal}

\displaystyle \angle3=\angle5,\qquad\angle4=\angle6.

\displaystyle \textbf{3. Alternate Exterior Angles are Equal}

\displaystyle \angle2=\angle8,\qquad\angle1=\angle7.

\displaystyle \textbf{4. Consecutive Interior Angles are Supplementary}

\displaystyle \angle4+\angle5=180^\circ,

\displaystyle \angle3+\angle6=180^\circ.

\displaystyle \textbf{Converse Properties for Parallel Lines}

\displaystyle \text{The converse of each of the above properties can be used to establish that}
\displaystyle \text{two lines are parallel.}

\displaystyle \text{(i) If a pair of corresponding angles is equal, then the two lines are parallel.}

\displaystyle \text{(ii) If a pair of alternate interior angles is equal, then the two lines are}
\displaystyle \text{parallel.}

\displaystyle \text{(iii) If a pair of alternate exterior angles is equal, then the two lines are}
\displaystyle \text{parallel.}

\displaystyle \text{(iv) If a pair of consecutive interior angles is supplementary, then the two}
\displaystyle \text{lines are parallel.}

\displaystyle \textbf{Important Properties of Parallel Lines}

\displaystyle \text{(i) Two distinct intersecting lines cannot both be parallel to the same line.}

\displaystyle \text{(ii) Two distinct lines parallel to the same line are parallel to each other.}

\displaystyle \text{Thus, if }l\parallel n\text{ and }m\parallel n,\text{ then }l\parallel m.

\displaystyle \text{(iii) Through a point not lying on a given line, exactly one line can be drawn}
\displaystyle \text{parallel to the given line.}

Discover more from ICSE / ISC / CBSE Mathematics Portal for K12 Students

Subscribe to get the latest posts sent to your email.