Class 8: Relations and Mapping (Lecture Notes – 1) – ICSE / ISC / CBSE Mathematics Portal for K12 Students

Ordered Pair

Two elements $a \ and \ b$ listed in a specific order, form an ordered pair, denoted by $a \ and \ b$ .

In an ordered pair $a \ and \ b$ , we call a as the first component and b as the second component.

By changing the positions of the components, the ordered pair is changed, i.e. $(5, \ 4) \ne (4, \ 5)$

Also if $(a, \ b) = (c, d) \Rightarrow a=c \ and \ b=d$

Thus $(a, \ b) = (2, 7) \Rightarrow a=2 \ and \ b=7$

$\\$

Cartesian Product of Two Sets

Let $A \ and \ B$ be two non-empty sets. Then their Cartesian product $A \ \times \ B$ is the set of all ordered pairs $a \ and \ b$ such that $a \in A \ and\ b\in B.$

Example 1:

Let $A=\{a,\ b \} \ and \ B=\{1, \ 2, \ 3\}$

Then $A \times B = \{a,\ b \} \times \{1, \ 2, \ 3\} = \{ (a, 1), \ (a, 2),\ (a, 3),\ (b, 1),\ (b, 2),\ (b, 3)\}$

Relation

Let $A \ and \ B$ be two non-empty sets. Then every subset of $A \times B$ is called a relation from $A \ to\ B$ . i.e., if $R \subseteq A\times B$ , then $R$ is a relation from $A \ to \ B$

Representation of a Relation

Roster Form: When a relation is represented by the set of all ordered pairs contained in it, then it is said to be in roster form.

Example 2:

If $A=\{1, 9, 16, 25\} \ and\ B=\{1, 2, 3, 4, 5\}$ then a relation $R \ from\ A \ to\ B$ defined as ‘is the square of’ can be represented in the roster form as:

$R = \{(1,1), (9,3), (16, 4), (25, 5)\}$

You will notice that the first component of each subset is square of the second component of the subset.

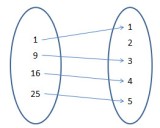
Arrow Diagram: Let $R$ be a relation from $A \ to \ B$ . We can draw the sets as shown pictorially. Then, we draw arrows from $A \ to \ B$ to indicate the pairing of the corresponding elements related to each other. Thus, we can show the relation given in Example 2 by the arrow diagram as shown.

Set Builder Form: A relation $R$ from $A \ to \ B$ is said to be in a Set-Builder form when written as:

$R=\{(a,\ b): a \in A,\ b \in B\ and\ a \ is \ connected \ with \ b \ by \ a \ given rule\}$

The relation given in Example 2 can be represented in the set-builder form as:

$R=\{(a,\ b): a \in A,\ b \in B\ and\ a=b^2\}$

Domain and Range of a Relation

Let $R$ be a relation from $A \ to \ B$ . Then,

Domain ( $R$ ) = Set of first components of all ordered pairs in $R$

Range ( $R$ ) = Set of second components of all ordered pairs in $R$

Rule of Relation

The property that tells us how the first component is related to the second component of each ordered pair in $R$ , is called the rule of the relation.

Let’s look at the following example:

Example 3:

Let $A=\{2,\ 3,\ 4\} \ and\ B=\{1, \ 3, \ 5\}$