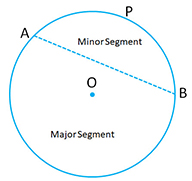
 Arc and it’s types:
Arc and it’s types:
- An arc is any part of the circumference.
- A chord divides the circumference of a circle in two parts or two arcs.
- The arc which is less than the semi-circle is called minor arc while the one that is larger then than the semi-circle is called major arc.
- A segment is the part of the circle bounded by an arc and a chord.
Theorem 9: The angle which an arc of a circle subtends at the center is double that which it subtends on any point of the part of the circumference.
Given: is the center of the given circle.
subtends
at the center and
at a point
on the circumference.
To Prove:
Proof: In ,
(Radius of the same circle)
Therefore (angle opposite to the equal sides of a triangle are equal)
(exterior angle of a
sum of the opposite interior angles)
Similarly in
Hence
.
Hence Proved.
Similarly, if you look at the following figures you will see that:


i)
ii)
Theorem 10: Angles in the same segment of a circle are equal.
Given: A center with center .
are in the same segment of the circle.

To Prove:
Proof: From Theorem 9, we know that
(angle at the center is twice the angle at the remaining circumference)
Similarly (angle at the center is twice the angle at the remaining circumference)
This implies that .
Hence Proved.
Similarly, in the adjoining figure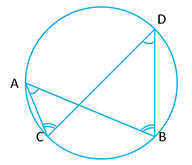
i) (Angles in the same segment)
ii) (Angles in the same segment)
Theorem 11: The angle in a semi circle is a right angle.
Given: A circle with center .
is the diameter and
is the angle of semi- circle.
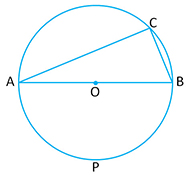
To Prove:
Proof: (angle at the center is twice the angle at the remaining circumference)
Given (straight line)
.
Hence Proved.
Cyclic Properties
Theorem 12: The opposite angles of a cyclic quadrilateral inscribed in a circle are supplementary.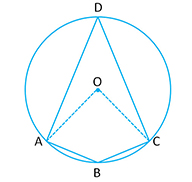
Given: A circle with center . A quadrilateral
inscribed in a circle.
To Prove:
Proof: (angle at the center is twice the angle at the remaining circumference)
Adding the two
Similarly we can prove that .
Hence Proved.
Note: 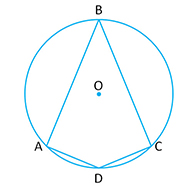
- If the opposite angles of a quadrilateral are supplementary, then the quadrilateral is cyclic
- The angle in the major segment is acute and the angle in the minor segment is obtuse. i.e.
while
Theorem 13: The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.
Given: Circle with center is the cyclic quadrilateral.
To Prove:
Proof: (the two angles are supplementary)
(Opposite angles of a a cyclic quadrilateral are supplementary…Theorem 12)
Therefore
Hence Proved.
Note: Take a look at the adjoining figure. You will see that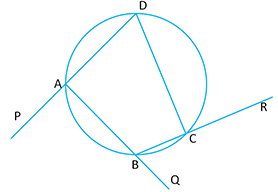
i)
ii)
iii)
