Class 10: Similarity – Exercise 16(a) – ICSE / ISC / CBSE Mathematics Portal for K12 Students

Question 1: State True or False:

(i) Two similar polygons are necessarily congruent – False

(ii) Two congruent polygons are necessarily similar – True

(iii) All equiangular triangles are similar – True

(iv) All isosceles triangles are similar – False

(v) Two isosceles right angles triangles are similar – True

(vi) Two isosceles triangles are similar if an angle of one is congruent to the corresponding angle of the other – True

(vii) The diagonals of the trapezium, divide each into proportional segments – True

$\displaystyle \\$

Question 2: $\displaystyle \text{In } \triangle ABC, DE \parallel BC$ , where $\displaystyle D \text{ and } E$ are points on $\displaystyle AB \text{ and } AC$ respectively. Prove that $\displaystyle \triangle ADE \sim \triangle ABC .$ Also find the length of $\displaystyle DE, if AD = 12 \text{ cm,} BD = 24 \text{ \text{ cm } } \text{ and } BC = 8 \text{ cm}.$

Answer:

$\displaystyle \text{In } \triangle ABC, DE \parallel BC$

$\displaystyle \text{Consider } \triangle ABC \text{ and } \triangle ADE$

$\displaystyle \angle ABC = \angle ADE \text{ (alternate angles) }$

$\displaystyle \angle ACB =\angle AED \text{ (alternate angles) }$

$\displaystyle \text{Therefore } \triangle ADE \sim \triangle ABC \text{ (AAA postulate) }$

$\displaystyle \text{Hence } \frac{AD}{AB} = \frac{DE}{BC} = \frac{AE}{AC}$

$\displaystyle \frac{12}{12+24} = \frac{DE}{8}$

$\displaystyle \Rightarrow DE = \frac{12}{36} \times 8 = \frac{8}{3}$

$\displaystyle \\$

Question 3: $\displaystyle \text{Given } \angle GHE = \angle DFE= 90^{\circ}$ , $\displaystyle DH= 8, DF=12, DG=3x-1 \text{ and } DE=4x+2 .$ Find the length of the segments $\displaystyle DG \text{ and } DE.$

Answer:

$\displaystyle \text{Consider } \triangle EFD \text{ and } \triangle GHD$

$\displaystyle \angle GHE = \angle DFE= 90^{\circ} \text{ (Given) }$

$\displaystyle \angle EDG = \angle HDG (\angle D \text{ is common } )$

$\displaystyle \text{Therefore } \triangle EFD \sim \triangle GHD \text{ (AAA postulate) }$

$\displaystyle \frac{DH}{DF} = \frac{DG}{DE}$

$\displaystyle \frac{8}{12} = \frac{3x-1}{4x+2}$

$\displaystyle 32x+16 = 36x-12$

$\displaystyle 4x=28 \Rightarrow x = 7$

$\displaystyle \text{Substituting } DG = 3 \times 7 -1 = 20$

$\displaystyle DE = 4 \times 7 +2 = 30$

$\displaystyle \\$

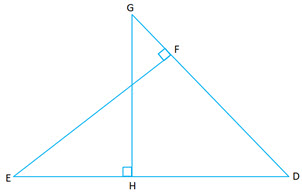
Question 4: $\displaystyle D$ is a point of side $\displaystyle BC$ of $\displaystyle \triangle ABC$ such that $\displaystyle \angle ADC = \angle BAC .$ Prove that $\displaystyle CA^2=CB \times CD .$

Answer:

$\displaystyle \text{Consider } \triangle ABC \text{ and } \triangle ADC$

$\displaystyle \angle BAC = \angle ADC \text{ (Given) }$

$\displaystyle \angle ACB = \angle ACD (\angle C \text{ is common } )$

$\displaystyle \text{Therefore } \triangle ABC \text{ and } \triangle ADC \text{ (AAA postulate) }$

$\displaystyle \text{Therefore } \frac{CA}{CB} = \frac{CD}{CA}$

$\displaystyle \Rightarrow CA^2=CB \times CD$

$\displaystyle \\$

Question 5: In the given figure, $\displaystyle \triangle ABC \text{ and } \triangle AMP$ are right angled at $\displaystyle B \text{ and } M$ respectively. $\displaystyle \text{Given } AC=10 \text{ cm,} AP = 15 \text{ cm } \text{ and } PM= 12 \text{ cm}.$

(i) Prove $\displaystyle \triangle ABC \sim \triangle AMP$ (ii) Find $\displaystyle AB \text{ and } AC$ [2012]

Answer:

$\displaystyle \text{In } \triangle ABC \text{ and } \triangle AMP$

$\displaystyle \angle BAC = \angle PAM \text{ (common angle) }$

$\displaystyle \angle ABC =\angle PMA$

$\displaystyle \text{Therefore } \triangle ABC \sim \triangle AMP \text{ (AAA postulate) }$

$\displaystyle \text{Since } \triangle ABC \sim \triangle AMP$

$\displaystyle \frac{AP}{AM} = \frac{BC}{PM} = \frac{AC}{AP}$

$\displaystyle \text{Given } AC=10 \text{ cm,} AP = 15 \text{ cm } \text{ and } PM= 12 \text{ cm }$

$\displaystyle \Rightarrow AB = \frac{10}{15} \times 11 = 7.33 \text{ cm }$

$\displaystyle \Rightarrow BC = \frac{10}{15} \times 12 = 8 \text{ cm }$

$\displaystyle \\$

Question 6: $\displaystyle E \text{ and } F$ are points in sides $\displaystyle DC \text{ and } AB$ respectively of parallelogram $\displaystyle ABCD .$ If diagonal $\displaystyle AC$ and segment $\displaystyle EF$ intersect at $\displaystyle G$ ; prove that: $\displaystyle AG \times EG = FG \times CG .$

Answer:

$\displaystyle \text{In } \triangle AGF \text{ and } \triangle EGC$

$\displaystyle \angle AGF = \angle EGC \text{ (opposite angles) }$

$\displaystyle \angle ECG =\angle FAG \text{ (alternate angles) }$

$\displaystyle \text{Therefore } \triangle AGF \sim \triangle ECG \text{ (AAA postulate) }$

$\displaystyle \text{Therefore } \frac{EG}{FG} = \frac{CG}{AG}$

$\displaystyle \Rightarrow AG \times EG = FG \times CG$

$\displaystyle \\$

Question 7: $\displaystyle \text{Given } RS \text{ and } PT$ are altitudes of $\displaystyle \triangle PQR .$ Prove that $\displaystyle \text{(i) } \triangle PQT \sim \triangle QRS \hspace{1.0cm} \text{(ii) } PQ \times QS = RQ \times QT$

Answer:

$\displaystyle \text{(i) } \text{Consider } \triangle PQT \text{ and } \triangle QRS$

$\displaystyle \angle QTP = \angle QSR= 90^{\circ}$ (Given, altitudes)

$\displaystyle \angle PQT = \angle SQR \ \ \ (\angle Q \text{ is common } )$

$\displaystyle \text{Therefore } \triangle PQT \sim \triangle QRS \text{ (AAA postulate) }$

$\displaystyle \text{(ii) } \frac{PQ}{RQ} = \frac{QT}{QS}$

$\displaystyle PQ \times QS = RQ \times QT$

$\displaystyle \\$

Question 8: $\displaystyle \text{Given } ABCD$ is a rhombus, $\displaystyle DPR \text{ and } CBR$ are straight lines. Prove that $\displaystyle DP \times CR = DC \times PR .$

Answer:

$\displaystyle \text{In } \triangle DPA \text{ and } \triangle RPC$

$\displaystyle \angle DPA = \angle RPC \text{ (vertically opposite angles) }$

$\displaystyle \angle PAD =\angle PCR \text{ (alternate angles) }$

$\displaystyle \text{Therefore } \triangle DPA \sim \triangle RPC \text{ (AAA postulate) }$

$\displaystyle \text{Therefore } \frac{DB}{PR} = \frac{AD}{CR}$

$\displaystyle \frac{DP}{PR} = \frac{DC}{CR} \ \ \ ( AD = DC \text{ as } ABCD \text{ is a Rhombus} )$

$\displaystyle \Rightarrow DP \times CR = DC \times PR$

$\displaystyle \\$

$\displaystyle \text{Question 9: Given } FB=FD, AE \perp FD \text{ and } FC \perp AD . \\ \\ \text{Prove } \frac{GB}{AD} = \frac{BC}{ED}$

Answer:

$\displaystyle FB=FD, AE \perp FD \text{ and } FC \perp AD .$

$\displaystyle \text{Therefore } \angle FDB=\angle FBD$

$\displaystyle \text{Consider } \triangle AED \text{ and } \triangle FCB$

$\displaystyle \angle AED = \angle FCB= 90^{\circ} \text{ (Given) }$

$\displaystyle \angle ADE = \angle FBC$

$\displaystyle \text{Therefore } \triangle AED \sim \triangle FBC \text{ (AAA postulate) }$

$\displaystyle \frac{AD}{FB} = \frac{ED}{BC}$

$\displaystyle \frac{FB}{AD} = \frac{BC}{ED}$

$\displaystyle \\$

Question 10: $\displaystyle \text{In } \triangle ABC, \angle B = 2 \angle C$ and the bisector of $\displaystyle \angle B$ meets $\displaystyle CA$ at point $\displaystyle D .$ Prove that $\displaystyle \text{(i) } \triangle ABC \sim \triangle ABD \hspace{1.0cm} \text{(ii) } DC:AD = BC:AB$

Answer:

$\displaystyle \text{Given } \triangle ABC, \angle B = 2 \angle C$

$\displaystyle \angle ABD = \angle DBC$

$\displaystyle \text{Therefore } \angle ABD = \angle DBC = \angle ACB$

$\displaystyle \text{Consider } \triangle ABC \text{ and } \triangle ABD$

$\displaystyle \angle BAC = \angle DAB \text{ (Given) }$

$\displaystyle \angle ACB = \angle ABD$

$\displaystyle \text{Therefore } \triangle ABC \sim \triangle ABD \text{ (AAA postulate) }$

$\displaystyle \frac{BC}{BD} \frac{AB}{AD}$

$\displaystyle \frac{BC}{AB} = \frac{BD}{AD}$

$\displaystyle \frac{BC}{AB} = \frac{DC}{AD}$ ( $\displaystyle \angle DBC = \angle DCB \Rightarrow DC = BD$ )

$\displaystyle DC:AD = BC:AB$

$\displaystyle \\$

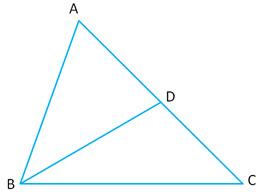
Question 11: $\displaystyle \text{In } \triangle PQR, \angle Q=90^{\circ} \text{ and } QM \perp PR .$ Prove that:

$\displaystyle \text{(i) } PQ^2 = PM \times PR$

$\displaystyle \text{(ii) } QR^2 = PR \times MR$

$\displaystyle \text{(iii) } PQ^2 + QR^2 = PR^2$

Answer:

$\displaystyle \text{(i) } \text{Given } \triangle PQR, \angle Q=90^{\circ} \text{ and } QM \perp PR$

$\displaystyle \text{Consider } \triangle PQM \text{ and } \triangle PRQ$

$\displaystyle \angle PMQ = \angle PQR = 90^{\circ} \text{ (Given) }$

$\displaystyle \angle QPM =\angle RPQ \text{ (common angle) }$

$\displaystyle \text{Therefore } \triangle PQM \sim \triangle PRQ \text{ (AAA postulate) }$

$\displaystyle \text{Hence } \frac{PQ}{PR} = \frac{PM}{PQ}$

$\displaystyle \text{Therefore } PQ^2 = PM \times PR$

$\displaystyle \text{(ii) } \text{Consider } \triangle QMR \text{ and } \triangle PQR$

$\displaystyle \angle QMR = \angle PQR = 90^{\circ} \text{ (Given) }$

$\displaystyle \angle QRM =\angle QRP \text{ (common angle) }$

$\displaystyle \text{Therefore } \triangle QMR \sim \triangle PQR \text{ (AAA postulate) }$

$\displaystyle \text{Hence } \frac{QR}{PR} = \frac{MR}{QR}$

$\displaystyle \text{Therefore } QR^2 = PR \times MR$

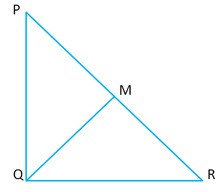
(iii) Adding (i) and (ii)

$\displaystyle PQ^2 + QR^2 = PM \times PR + PR \times MR$

$\displaystyle \Rightarrow PQ^2 + QR^2 = PR \times (PM + MR)$

$\displaystyle \Rightarrow PQ^2 + QR^2 = PR \times PR = PR^2$

$\displaystyle \\$

Question 12: $\displaystyle \text{In } \triangle ABC, \angle C= 90^{\circ}, CD \perp AB .$ Prove that $\displaystyle CD^2 = AD \times DB .$

Answer:

$\displaystyle \triangle ABC, \angle C= 90^{\circ}, CD \perp AB .$

$\displaystyle \text{Consider } \triangle PQM \text{ and } \triangle PRQ$

$\displaystyle \angle PMQ = \angle PQR = 90^{\circ} \text{ (Given) }$

$\displaystyle \angle QPM =\angle RPQ \text{ (common angle) }$

$\displaystyle \text{Therefore } \triangle PQM \sim \triangle PRQ \text{ (AAA postulate) }$

$\displaystyle \text{Hence } \frac{PQ}{PR} = \frac{PM}{PQ}$

$\displaystyle \text{Therefore } PQ^2 = PM \times PR$

$\displaystyle \\$

Question 13: $\displaystyle \text{In } \triangle ABC, \angle B= 90^{\circ}, BD \perp AC .$

$\displaystyle \text{(i) If } CD=10 \text{ cm } \text{ and } BD = 8 \text{ cm, Find } AD$

$\displaystyle \text{(ii) If } AC=18 \text{ cm } \text{ and } AD = 6 \text{ cm, Find } BD$

$\displaystyle \text{(iii) If } AC=9 \text{ cm } \text{ and } AB = 7 \text{ cm, Find } AD$

Answer:

$\displaystyle \triangle ABC, \angle B= 90^{\circ}, BD \perp AC$

$\displaystyle \text{Consider } \triangle CDB \text{ and } \triangle BCD$

$\displaystyle \angle ADB = \angle BDC = 90^{\circ} \text{ (Given) }$

$\displaystyle \angle ABD =\angle BCD$

$\displaystyle \text{Therefore } \triangle CDB \sim \triangle BDA \text{ (AAA postulate) }$

$\displaystyle \text{(i) } \frac{CD}{BD} = \frac{BD}{AD}$

$\displaystyle \text{Therefore } AD = \frac{BD^2}{CD} = \frac{8^2}{10} = 6.4 \text{ cm }$

$\displaystyle \text{(ii) } \frac{BD}{DA} = \frac{CD}{BD}$

$\displaystyle \text{Therefore } BD = \sqrt{CD \times DA} = \sqrt{72}= 8.49 \text{ cm }$

$\displaystyle \text{(iii) } \frac{AD}{AB} = \frac{AB}{AC}$

$\displaystyle \text{Therefore } AD = \frac{AB \times AB}{AC} = \frac{7 \times 7}{9} = 5.44 \text{ cm }$

$\displaystyle \\$

Question 14: In the figure, $\displaystyle PQRS$ is a parallelogram with $\displaystyle PQ=16 \text{ cm } \text{ and } QR=10 \text{ cm } .$ $\displaystyle L$ is a point on $\displaystyle PR$ such that $\displaystyle RL:LP=2:3 .$

$\displaystyle QL$ produced meets $\displaystyle RS$ at $\displaystyle M \text{ and } PS$ produced at $\displaystyle N .$ Find the lengths of $\displaystyle PN \text{ and } RM .$ [1997]

Answer:

$\displaystyle \text{In } \triangle RLQ \text{ and } \triangle PLN$

$\displaystyle \angle RLQ = \angle PLN \text{ (vertically opposite angles) }$

$\displaystyle \angle LRQ = \angle LPN \text{ (alternate angles) }$

$\displaystyle \text{Therefore } \triangle RLQ \sim \triangle PLN \text{ (AAA postulate) }$

$\displaystyle \text{Therefore } \frac{RL}{LP} = \frac{RQ}{PN}$

$\displaystyle \Rightarrow PN = \frac{10}{2} \times 3 = 15 \text{ cm }$

$\displaystyle \text{In } \triangle RLM \text{ and } \triangle PLQ$

$\displaystyle \angle RLM = \angle PLQ \text{ (vertically opposite angles) }$

$\displaystyle \angle LRM = \angle LPQ \text{ (alternate angles) }$

$\displaystyle \text{Therefore } \triangle RLM \sim \triangle PLQ \text{ (AAA postulate) }$

$\displaystyle \text{Therefore } \frac{RM}{PQ} = \frac{RL}{LP}$

$\displaystyle \Rightarrow RM = \frac{2}{3} \times 16 = 10.667 \text{ cm }$

$\displaystyle \\$

Question 15: In quadrilateral $\displaystyle ABCD$ , Diagonal $\displaystyle AC \text{ and } BD$ intersect at point $\displaystyle E$ such that: $\displaystyle AE:EC=BE:ED .$ Show that $\displaystyle ABCD$ is a parallelogram.

Answer:

$\displaystyle \text{Given } \frac{AE}{EC} = \frac{BE}{ED} .$ .. … … … (i)

$\displaystyle \text{In } \triangle ADB \text{, because } EF \parallel AB \text{, by proportionality theorem }$

$\displaystyle \frac{DF}{FA} = \frac{ED}{BE} .$ .. … … … (i)

Therefore from (i) and (ii)

$\displaystyle \frac{DF}{FA} = \frac{EC}{AE}$

Similarly $\displaystyle \text{In } \triangle DCA$

$\displaystyle \frac{DF}{FA} = \frac{CE}{AE} \Rightarrow FE \parallel DC$

Also it is given that $\displaystyle FE \parallel AB$

$\displaystyle \text{Therefore } DC \parallel AB .$ $\displaystyle \text{Therefore } ABCD \text{ is a parallelogram. }$

$\displaystyle \\$

Question 16: $\displaystyle \text{Given } AB \parallel DE \text{ and } BC \parallel EF .$ Prove that:

$\displaystyle \text{(i) } \frac{AD}{DG} = \frac{CF}{FG}$

$\displaystyle \text{(ii) } \triangle DFG \sim \triangle ACG$

Answer:

$\displaystyle \text{(i) } \text{Given } AB \parallel DE \text{ and } BC \parallel EF$

$\displaystyle \text{In } \triangle AGB, \frac{AD}{DG} = \frac{EB}{GE} .$ .. … … … (i)

$\displaystyle \text{In } \triangle BGC, \frac{EB}{GE} = \frac{CF}{FG} .$ .. … … … (ii)

$\displaystyle \text{From (i) and (ii) you get } \frac{AD}{DG} = \frac{CF}{FG}$

$\displaystyle \text{(ii) } \text{Consider } \triangle DFG \text{ and } \triangle ACG$

$\displaystyle \text{We have } \frac{AD}{DG} = \frac{CF}{FG}$

and $\displaystyle \angle DGF = \angle AGC \text{ (common angle) }$

$\displaystyle \text{Therefore } \triangle DFG \sim \triangle ACG$

$\displaystyle \\$

Question 17: $\displaystyle \text{In } \triangle ABC, AD \perp BC \text{ and } AD^2 = BD \times DC .$ Show that $\displaystyle \angle BAC = 90^{\circ} .$

Answer:

$\displaystyle \text{Given } AD^2 = BD \times DC$

$\displaystyle \Rightarrow \frac{AD}{DC} = \frac{BD}{AD}$

Also $\displaystyle \text{Given } \angle ADB = \angle ADC = 90^{\circ}$

$\displaystyle \text{Therefore } \triangle DBA \sim \triangle DAC$ (SAS postulate)

$\displaystyle \text{Therefore } \angle C = \angle BAD$

$\displaystyle \angle B = \angle DAC$

Adding $\displaystyle \angle C + \angle B = \angle BAD + \angle DAC$

$\displaystyle \Rightarrow \angle A =\angle C + \angle B .$ .. … … (i)

We k $\displaystyle \text{Now } \angle A + \angle B + \angle C = 180^{\circ} .$ .. … … … (ii)

From (i) and $\displaystyle \text{(ii) } 2 \angle A = 180^{\circ}$

$\displaystyle \Rightarrow \angle A = 90^{\circ}$

$\displaystyle \\$

Question 18: In the given figure $\displaystyle AB \parallel EF \parallel DC$ ; $\displaystyle AB=67.5 \text{ cm,} DC = 40.5 \text{ cm } \text{ and } AE = 52.5 \text{ cm } .$

(i) Name the three pairs of similar triangles

(ii) Find the lengths of $\displaystyle EC \text{ and } EF$

Answer:

$\displaystyle \text{Given } AB \parallel EF \parallel DC$ , The three pairs of similar triangles are

$\displaystyle \triangle ABC \sim \triangle CEF$

$\displaystyle \triangle BCD \sim \triangle BEF$

$\displaystyle \triangle ABE \sim \triangle CDE$

$\displaystyle \text{Since } \triangle ABE \sim \triangle CDE$

$\displaystyle \frac{AB}{CD} = \frac{AE}{CE} \Rightarrow CE = \frac{52.5 \times 40.5}{67.5} = 31.5 \text{ cm }$

$\displaystyle \text{Since } \triangle ABC \sim \triangle CEF$

$\displaystyle \frac{CE}{CA} = \frac{EF}{AB} \Rightarrow EF = \frac{67.5 \times 31.5}{52.5+31.5} = 25.3125 \text{ cm }$

$\displaystyle \\$

$\displaystyle \text{Question 19: In the given figure } QR \parallel AB \text{, and } DR \parallel QB. \\ \text{ Prove that } PQ^2 = PD \times PA.$

Answer:

$\displaystyle \text{Given } QR \parallel AB \text{, and } DR \parallel QB$

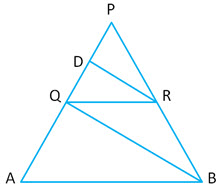
Using basic proportionality theorem

$\displaystyle \text{In } \triangle PQR \text{ and } \triangle PAB$

$\displaystyle \frac{PQ}{PA} = \frac{PR}{PB} .$ .. … … … (i)

$\displaystyle \text{In } \triangle PDR \text{ and } \triangle PQB$

$\displaystyle \frac{PD}{PQ} = \frac{PR}{PB} .$ .. … … … (ii)

From (i) and (ii) we get

$\displaystyle \frac{PQ}{PA} = \frac{PD}{PQ}$

$\displaystyle \Rightarrow PQ^2 = PD \times PA$

$\displaystyle \\$

Question 20: Through the mid point $\displaystyle M$ of the side $\displaystyle CD$ of a parallelogram $\displaystyle ABCD$ , the line $\displaystyle BM$ is drawn intersecting diagonal $\displaystyle AC \text{ in } L \text{ and } AD$ produced $\displaystyle \text{In } E .$ Prove that $\displaystyle EL=2BL .$

Answer:

$\displaystyle \text{Consider } \triangle DEM \text{ and } \triangle CBM$

$\displaystyle \angle AEB = \angle EBC \text{ (alternate angles) }$

$\displaystyle \angle EMD = \angle CMB \text{ (opposite angles) }$

$\displaystyle DM = MC$ (as M is the midpoint of CD)

$\displaystyle \text{Therefore } \triangle DEM \cong \triangle CBM$

$\displaystyle \text{Therefore } DE = BC \text{ (corresponding angles) }$

$\displaystyle AD = BC \text{ (opposite sides of a parallelogram) }$

$\displaystyle \text{Therefore } AE = AD + DE = 2BC$

$\displaystyle \text{Now } \text{Consider } \triangle ELA \text{ and } \triangle LBC$

$\displaystyle \angle AEB = \angle EBC$

$\displaystyle \angle ELA = \angle EBC$

$\displaystyle \text{Therefore } \triangle ELA \sim \triangle LBC$

$\displaystyle \text{Hence } \frac{EL}{BL} = \frac{EA}{BC}$

$\displaystyle \frac{EL}{BL} = \frac{2BC}{BC} = 2$

$\displaystyle \text{Hence } EL = 2 BL$

$\displaystyle \\$

Question 21: In the figure given below, $\displaystyle P$ is a point on $\displaystyle AB$ such that $\displaystyle AP:PB=4:3 .$ $\displaystyle PQ \parallel AC .$

(i) Calculate the ratio $\displaystyle PQ:AC$ , giving reasons for your answer.

$\displaystyle \text{(ii) } \text{In } \triangle ARC, \angle ARC = 90^{\circ} \text{ and } \text{In } \triangle PQS, \angle PSQ=90^{\circ} .$ $\displaystyle \text{Given } QS=6 \text{ cm }$ , calculate length of $\displaystyle AR .$ [1999]

Answer:

$\displaystyle \text{(i) } \text{Given } AP:PB=4:3$

Also $\displaystyle PQ \parallel AC$ , applying basic proportionality theorem

$\displaystyle \frac{AP}{PB} = \frac{CQ}{QB}$

$\displaystyle \Rightarrow \frac{CQ}{QB} = \frac{4}{3}$

$\displaystyle \Rightarrow \frac{BQ}{BC} = \frac{3}{7}$

$\displaystyle \angle QBP = \angle ACB \text{ (corresponding angles) }$

$\displaystyle \angle QPB = \angle CAB \text{ (corresponding angles) }$

$\displaystyle \text{Therefore } \triangle PBQ \sim \triangle ABC \text{ (AAA postulate) }$

$\displaystyle \frac{PQ}{ AC} = \frac{BQ}{ BC} = \frac{3}{ 7}$

$\displaystyle \text{(ii) } \text{Given } \angle ARC = \angle QSP = 90^{\circ}$

$\displaystyle \angle ACR = \angle SPQ \text{ (alternate angles) }$

$\displaystyle \text{Therefore } \triangle ARC \sim \triangle QSP \text{ (AAA postulate) }$

$\displaystyle \frac{AR}{ SQ} = \frac{AC}{ PQ} = \frac{7}{ 3}$

$\displaystyle \Rightarrow AR = \frac{7 \times 6}{3} = 14 \text{ cm }$

$\displaystyle \\$

Question 22: In the right angled $\displaystyle \triangle QPR, PM$ is the altitude. Given that $\displaystyle QR= 8 \text{ cm } \text{ and } MQ = 3.5 \text{ cm }$ , calculate the value of $\displaystyle PR .$ [2000]

Answer:

$\displaystyle \angle QPR = \angle PMR = 90^{\circ}$

$\displaystyle \angle PRQ = \angle PRM \text{ (common) }$

$\displaystyle \triangle PQR \sim \triangle MPR \text{ (AAA postulate) }$

$\displaystyle \frac{QR}{ PR} = \frac{ PR}{ MR}$

$\displaystyle PR^2 = QR \times MR = 8 \times 4.5 = 36 \Rightarrow PR = 6 \text{ cm }$

$\displaystyle \\$

Question 23: In the figure given below, median $\displaystyle BD \text{ and } CE$ of the $\displaystyle \triangle ABC$ meet at $\displaystyle G .$ Prove that: