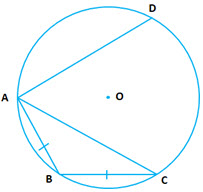
 Question 1: In the given diagram,
Question 1: In the given diagram, and AB = AC.
(i) What is the relation between and
?
(ii) What is the relation between and
?
(iii) If is greater than
, then what is the relation between the chord
and
?
(iv) If , find the measure of
.
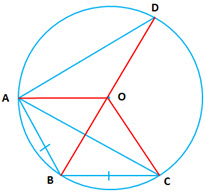 Answer:
Answer:
Given:
(i) (Since equal chords subtend equal arcs)
(ii) (equal arcs will subtend equal angles at the center)
(iii) If
Therefore
(iv) Given
Question 2: In , the
from vertices
and
on their opposite sides meet (when produced) the circumference of the triangle at points
and
respectively. Prove that:
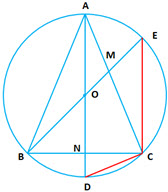 Answer:
Answer:
Consider &
(given)
(vertically opposite angles)
(AAA postulate)
Therefore
Therefore Arcs that subtend equal angle at circumference are equal
Therefore
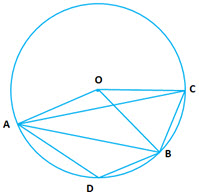
Question 3: In a cyclic trapezium, prove that non parallel sides are equal and the diagonals are also equals.
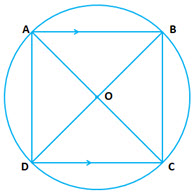 Answer:
Answer:
is a cyclic trapezium.
Chord subtends
at circumference
Chord subtends
at circumference
But (vertically opposite angles)
Therefore
Now in &
is common
(angles in the same segment)
(proved above)
(SAS axiom)
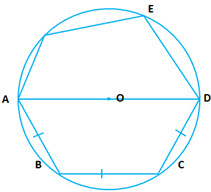 Question 4: In the given diagram,
Question 4: In the given diagram, is the diameter of the circle with center
. Chords
. If
, find (i)
(ii)
Answer:
Given
(i) is the diameter
(angle in semicircle)
(ii) Since (given)
(equal arcs subtend equal angles at center)
We know
In
(radius of the same circle)
Therefore
is a cyclic quadrilateral
(opposite angles are supplementary)
Now
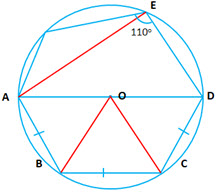
 Question 5: In the given diagram, if
Question 5: In the given diagram, if of circle with center
, prove that quadrilateral
is an isosceles trapezium.
Answer:
Given
(Equal arcs subtend equal angles at the circumference)
(alternate angles are equal)
Therefore is a trapezium
Also
Therefore is an Isosceles trapezium.

Question 6: In a given figure is an isosceles triangle and
is the center of the circumcircle. Prove
bisects
.
Answer:
Given (Since
is an isosceles triangle)
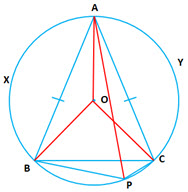
(equal chords subtend equal angles on the circumference)
Therefore bisects
.
Question 7: If two sides of a cyclic quadrilateral are parallel, prove that:
(i) its other two sides are equal
(ii) its diagonals are equal
Answer: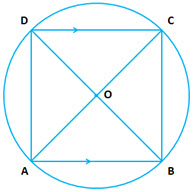
(i) Given
Therefore (alternate angles)
Chord subtends
on circumference.
Chord subtends
on circumference.
Therefore (since equal chords subtend equal angles on the circumference)
(ii) Consider
is common
(proved above)
(angles in the same segment)
Therefore (by SAS axiom)
Therefore (corresponding parts of congruent triangles are equal)
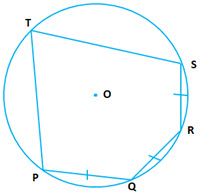 Question 8: In the given diagram, circle with center
Question 8: In the given diagram, circle with center .
and
. Calculate:
(i)
(ii)
(iii)
Answer:
Given 
(Equal chords subtend equal angles at the center of a circle)
(angle subtended at the center is twice that of the one subtended on the circumference)
In ,
(radius of the same circle)
Therefore
Similarly, in
and in
Therefore
(i)
(ii)
(iii)
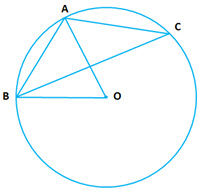 Question 9: In the given diagram,
Question 9: In the given diagram, is the side of regular six-side polygon and
is a side of a regular eight-sides polygon inscribed in a circle with center
. Calculate:
(i)
(ii)
(iii)
Answer:
(i) Since is the side of a regular hexagon
(ii) subtends
at the circumference and
at the center
(iii) Since is the side of a regular octagon
subtends
at the circumference and
at the center
Question 10: In a regular pentagon inscribed in a circle, find the ratio of the
[1990]
Answer: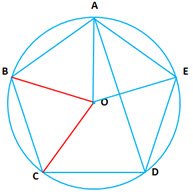
Consider
It subtends at the center and
at the circumference
Similarly, for we have
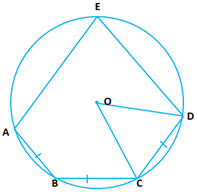 Question 11: In the given diagram,
Question 11: In the given diagram, and
. Find:
(i)
(ii)
(iii) [1993]
Answer:
Given
(equal arcs subtend equal angles at the center of a circle)
(i) In cyclic quadrilateral 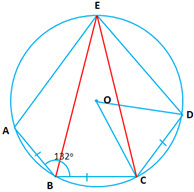
(opposite angles in a cyclic quadrilateral are supplementary)
Since (equal chords subtend equal angles on the circumference)
(ii) Since
(iii) subtends
at the center and
on the circumference
 Question 12: In the diagram,
Question 12: In the diagram, is the center of the circle and the length of
. If
find:
(i)
(ii) [1996]
Answer:
Given
(i)
(ii) (angle subtended at the center is twice that subtended at the circumference by a chord)
(iii) Similarly,
In cyclic quadrilateral
Question 13: In the diagram given below, is the center of the circle.
is the side of regular pentagon and
is the side of a regular hexagon. Find the angles of the
.
Answer:
is the side of a regular pentagon
is a side of regular hexagon
Now
subtends
at the center and
on the circumference
Similarly
Therefore
 Question 14: In the given diagram,
Question 14: In the given diagram, is the side of a regular hexagon,
is the side of a regular pentagon and
is a diameter. Calculate:
(i)
(ii)
(iii)
(iv) [1984]
Answer:
is a side of a regular hexagon
is a side of regular pentagon
(ii) In
(radius of the same circle)
(iii) In
(iv) In cyclic quadrilateral
(opposite angles of a cyclic quadrilateral are supplementary)
