Cone

Parameters of a Cone: Radius of the Base (r ), Height of the Cone (h ) and Slant Height of a Cone (l )

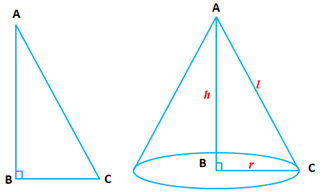
a1.jpg

Volume of a Cone = \frac{1}{3} \pi r^2 h

Curved surface area of a cone = \pi r l

Total surface area of a cone = Curved Surface area + Area of the base = \pi r^2+ \pi r l

Also note that l = \sqrt{r^2+h^2}

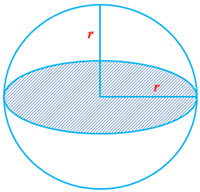
Spherea2.jpg

Parameters of a Sphere: Radius of the Sphere (r )

Volume of the sphere = \frac{4}{3} \pi  r ^3

Surface area of a sphere = 4 \pi r^2

Hemisphere

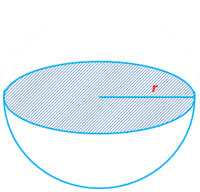a3Parameters of a Hemisphere: Radius of the Hemisphere (r )

Volume of the hemisphere = \frac{1}{2} \{\frac{4}{3} \pi  r ^3 \} = \frac{2}{3} \pi r^3

Total surface area of a hemisphere = \frac{1}{2} \{4 \pi r^2 \} + \pi r^2 = 3 \pi r^2

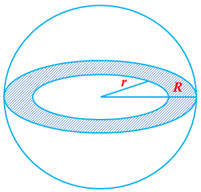a4 1Spherical Shell (hollow)

Parameters of a shell: Internal Radius of the Shell  (r ) and External Radius of the Shell (R )

Volume of the shell = \frac{4}{3} \pi (R^3-r^3) (this is also the volume of the material used to make the hollow shell)

External Surface are of spherical shell is the same as that of a sphere of radius R = 4 \pi R^2

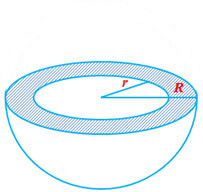a4Hemispherical Spherical Shell (hollow)

Parameters of a hemispherical shell: Internal Radius of the Shell (r ) and External Radius of the Shell (R )

Volume of the shell = \frac{2}{3} \pi (R^3-r^3) (this is also the volume of the material used to make the hollow shell)

Total surface are of the shell = outside surface area of the shell + Inside surface area of the shell +area of the ring

= \frac{1}{2} (4\pi R^2) +  \frac{1}{2} (4\pi r^2) + (\pi R^2 - \pi r^2)

= 2 \pi (R^2+r^2) + \pi (R^2-r^2) = 3 \pi R^2 + \pi r^2

a5

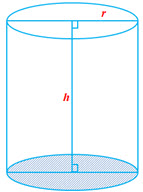
Cylinder

Parameters of a Cylinder: Radius (r) of the base and Height (h) of the Cylinder.

Area of cross section of a cylinder = \pi r^2

Perimeter of the cross section = 2 \pi r

Volume of the cylinder = \pi r ^2 h 

Curved surface area = 2 \pi r h

Total surface are of a solid cylinder = 2 \pi r h + 2 \pi r^2 = 2 \pi r (r + h)

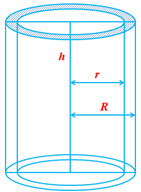a6Hollow Cylinder

Parameters of a hollow cylinder: Internal Radius (r) , External Radius (R) , Height (h)

Thickness of the wall of the cylinder = (R- r)

Area of the cross section = \pi R^2 - \pi r^2 = \pi (R^2-r^2)

Volume of the material use to make the hollow cylinder = External volume – Internal volume = \pi R^2 h - \pi r^2 h = \pi  (R^2-r^2) h

External curved surface area = 2 \pi R h

Internal curved surface area = 2 \pi r h

Total surface area = External curved surface area + Internal curved surface area  + 2 (Area of cross section) =  2 \pi R h + 2 \pi r h + 2 \pi (R^2-r^2)