Class 9: Triangles – Exercise 9.1 – ICSE / ISC / CBSE Mathematics Portal for K12 Students

Question 1: In the adjoining figure, $X$ and $Y$ are two points on equal sides $AB$ and $AC$ of $\triangle ABC$ such that $AX = AY$ . Prove that $AC = YB$ .

Answer:

Consider $\triangle AYB$ and $\triangle AXC$

$AX = AY$ (given)

$\angle A$ is common

$AB = AC$ (given)

Therefore $\triangle AYB \cong \triangle AXC$ (by S.A.S theorem)

Hence $XC = YB$

$\\$

Question 2: If $D$ is the mid point of the hypotenuse $AC$ of a right triangle $ABC$ , prove that $BD =\frac{1}{2} AC$ .

Answer:

Construct ABD such that ABD = DE

Consider $\triangle ABD$ and $\triangle ECD$

$AD = DC$ (given)

$\angle ADB = \angle EDC$ (vertically opposite angles)

$BD = DE$ (constructed)

Therefore $\triangle ABD \cong \triangle EDC$ (by S.A.S theorem)

$\Rightarrow EC = AB$ and $\angle ABD = \angle CED$

$\Rightarrow CE \parallel AB$

$\Rightarrow \angle ABC + \angle ECB = 180^o$ (interior angles on the same side of the transversal are supplementary)

$\Rightarrow 90^o + \angle ECB = 180 \Rightarrow \angle ECB = 90^o$

Therefore $\triangle ABC$ and $\triangle ECB$ are right angle triangles.

Therefore $\angle ABC = \angle ECB$

$BC$ is common

$AB = EC$

Therefore $\triangle ABC \cong \triangle ECB$

$\Rightarrow AC = BE$

$\Rightarrow \frac{1}{2} AC = \frac{1}{2} BE = BD$ . Hence proved.

$\\$

Question 3: In a quadrilateral $ACBD, \ AC = AD$ and $AB$ bisects $\angle A$ . Show that $\triangle ABC \cong \triangle ABD$ . What can you say about $BC$ and $BD$ .

Answer:

Consider $\triangle ABC$ and $\triangle ABD$

$AC = AD$ (given)

$\angle CAB = \angle DAB$ (given)

$AB$ is common

Therefore $\triangle ABC \cong \triangle ABD$ (by S.A.S theorem)

$\Rightarrow BC = BD$

$\\$

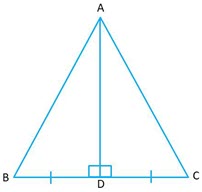Question 4: Prove that $\triangle ABC$ is isosceles if any of the following holds: (i) Altitude $AD$ bisects $BC$ (ii) Median $AD$ is perpendicular to the base $BC$ .

Answer:

(i) If $BD = DC$

Consider $\triangle ADB$ and $\triangle ADC$

$AD$ is common

$\angle ADB = \angle ADC = 90^o$ (altitude is perpendicular to the base)

$BD = DC$ (given)

Therefore $\triangle ADB \cong \triangle ADC$

Therefore $AB = AC \Rightarrow \triangle ABC$ is isosceles triangle.

(ii) If Median $AD$ is perpendicular to the base $BC$

$\angle ADB = \angle ADC = 90^o$

$AD$ is common

$BD = DC$ (since $AD$ is the median, $D$ is the midpoint of $BC$ )

Therefore $\triangle ADB \cong \triangle ADC$

Therefore $AB = AC \Rightarrow \triangle ABC$ is isosceles triangle.

$\\$

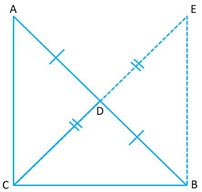
Question 5: In the adjoining figure $PS = QR$ and $\angle SPQ = \angle RQP$ . Prove that $\triangle PQS \cong \triangle QPR$ , $PR = QS$ and $\angle QPR = \angle PQS$ .

Answer:

Consider $\triangle PQS$ and $\triangle PQR$

$PS=QR$ is given

$\angle SPQ = \angle RQP$ given

$PQ$ (is common)

Therefore $\triangle PQS \cong \triangle PQR$

Therefore $PR = QS$ and $\angle QPR = \angle PQS$

$\\$

Question 6: In the adjoining figure, $AC = AE$ , $AB = AD$ and $\angle BAD = \angle EAC$ . Prove that $BC = DE$

Answer:

Given $\angle BAD = \angle EAC$ , $AE = AC$ and $AB = AD$

$\angle BAD + \angle DAC = \angle DAC + \angle CAE$

Therefore $\triangle ABC \cong \triangle ADE$ (by S.A.S theorem)

$\\$

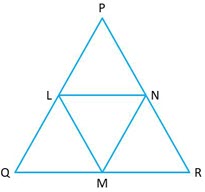Question 7: In a $\triangle PQR, if PQ = QR$ , and $L, M$ and $N$ are midpoints of the sides $PQ, QR$ and $RP$ respectively. Prove that $LN = MN$ .

Answer:

Given $PQ = QR$

$\Rightarrow PL = LQ = QM = MR$

$PN = NR$

Consider $\triangle PLN$ and $\triangle MNR$

$PL = MR$

$PN = NR$

$\angle P = \angle R$

$\therefore \triangle PLN \cong \triangle MNR$

Therefore $LN = LM$

$\\$

Question 8: In the adjoining figure, $PQRS$ is a square and $SRT$ is an equilateral triangle. Prove that (i) $PT=QT$ (ii) $\angle TQR = 15^o$

Answer:

Consider $\triangle PST$ and $\triangle QRT$

$ST = RT$ (equilateral triangle)

$SP = RQ$ (sides of a square)

Since $\angle PST = 60^o+90^o = 150^o$ and $\angle QRT = 60^o+90^o = 150^o$

$\angle PST = \angle QRT$

Therefore $\triangle PST \cong \triangle QRT$

In $\triangle TQR$

$RT = RQ$

Therefore $\angle QTR = \angle TQR = x$

$\Rightarrow 2x+ 150 = 180 \Rightarrow x = 15^o$

$\\$

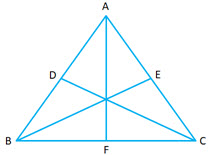2018-07-13_20-42-58 Question 9: Prove that the median of an equilateral triangle are equal.

Answer:

Given: $AD = DB, BF = FC, AE = EC$

$\triangle ABC$ is equilateral

Therefore $\angle A = \angle B = \angle C = 60^o$

To prove: $AF = BE = CD$

Consider $\triangle ABE$ and $\triangle DBC$

$AB = BC ( \triangle ABC$ is an equilateral triangle)

$\angle A = \angle B ( \triangle ABC$ is an equilateral triangle)

$AE = DB$ (medians bisect the opposite side. Since $\triangle ABC$ is an equilateral triangle the sides are equal)

Therefore $\triangle ABE \cong \triangle DBC$

Now consider $\triangle ADC$ and $\triangle BEC$

$\angle A = \angle C ( \triangle ABC$ is an equilateral triangle)

$AD=EC$

$AC=BC ( \triangle ABC$ is an equilateral triangle)

Therefore $\triangle ADC \cong \triangle BEC$

Hence $DC = BE$

Hence we can say that $AD = EC = BE$

$\\$

Question 10: $AB$ is a line segment. $P$ and $Q$ are points on opposite sides of $AB$ such that each of them is equidistant from the points $A$ and $B$ . Show that the line $PQ$ is perpendicular bisector of $AB$ .

Answer:

Consider $\triangle APC$ and $\triangle BPC$

$AP = BP$ (given)

$\angle APC = \angle BPC$ (bisector)

$PC$ is common

Therefore $\triangle APC \cong \triangle BPC$

Therefore $\angle PCA = \angle PCB = x$

$\Rightarrow 2x = 180 \Rightarrow x = 90^o$

Similarly in $\triangle ACQ$ and $\triangle BCQ$

$AQ = BQ$

$\angle AQC = \angle BQC$

$CQ$ is common

Therefore $\triangle ACQ \cong \triangle BCQ$

$\Rightarrow \angle ACQ = \angle BCQ = y$

$\Rightarrow 2y = 180 \Rightarrow 90^o$

Therefore $PC$ is a perpendicular bisector of $AB$

$\\$

Question 11: In the adjoining figure, $AB = AC$ and $DB = DC$ , find the ratio $\angle ABD : \angle ACD$

Answer:

Since $AB = AC \Rightarrow \angle ABC = \angle ACB$

Also since $BD = CD \Rightarrow \angle DBC = \angle DCB$

Now $\angle ABC = \angle ACB$

$\Rightarrow \angle ABD + \angle DBC = \angle ACD + \angle DCB$

$\Rightarrow \angle ABD = \angle ADC$

$\\$

2018-07-14_19-22-31 Question 12: In the adjoining figure, $\angle BCD = \angle ADC$ and $\angle ACB = \angle BDA$ . Prove that $AD = BC$ and $\angle CAD = \angle CBD$ .

Answer:

Given: $\angle BCD = \angle ADC$

Since $\angle ACB = \angle BDA$

Therefore $\angle BCD + \angle ACB = \angle ADC + \angle BDA$

$\Rightarrow \angle ACD = \angle BDC$

Therefore in $\triangle ACD$ and $\triangle BDC$ , we have

$\angle ADC = \angle BCD$

$CD$ is common

$\angle ACD = \angle BDC$

Therefore $\triangle ACD \cong \triangle ABD$ (A.S.A. theorem)

Hence $AD = BC$ and $\angle CAD = \angle CBD$

$\\$

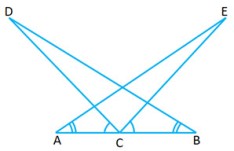2018-07-14_19-23-21 Question 13: In the adjoining figure, $AC = BC, \angle DCA = \angle ECB$ and $\angle DBC = \angle EAC$ . Prove that $\triangle DBC \cong \triangle EAC$ and hence $DC = EC$ and $latex $latex $BD = AE$ .

Answer:

Given: $\angle DCA = \angle ECB$

$\Rightarrow \angle DCA + \angle ECD = \angle ECB + \angle ECD$

$\Rightarrow \angle ECA = \angle DCB$

Consider $\triangle DBC$ and $\triangle EAC$

$\angle DCB = \angle EAC$ (Proved above)

$BC = AC$ (given)

$\angle DBC = \angle EAC$ (given)

Therefore $\triangle DBC \cong \triangle EAC$ (A.S.A theorem)

Therefore $DC = EC$ and $BD = AE$

$\\$

Question 14: In the adjoining figure, it is given that $CE = ED, \angle AOC = 2 \angle BCD$ and $\angle BOD = 2 \angle ADC$ . Prove that $\triangle CBE \cong \triangle DAE$ .

Answer:

Consider $\triangle CED$ , we have

$CE = DE \Rightarrow \angle EDC = \angle ECD$ … … … … … (i)

We have $\angle AOC = \angle BOD$ (vertically opposite angles)

$\Rightarrow 2 \angle BCD = 2 \angle ADC$

$\Rightarrow \angle BCD = \angle ADC$ … … … … … (ii)

Subtracting (ii) from (i) we get

$\angle ECD - \angle BCD = \angle EDC - \angle ADC$

$\Rightarrow \angle ECB = \angle EDA$

Therefore in $\triangle CBE$ and $\triangle DAE$ , we have

$\angle CEB = \angle DEA$ (common angle)

$CE = DE$ (given) and

$\angle ECB = \angle EDA$

Therefore $\triangle CBE \cong \triangle DAE$ (A.S.A. theorem)

$\\$

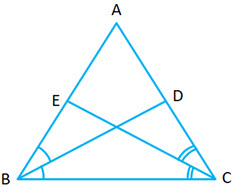2018-07-14_19-24-48 Question 15: $BD$ and $CE$ are bisectors of $\angle ABC$ and $\angle ACB$ of an isosceles $\triangle ABC$ with $AB = AC$ . Prove that $BD = CE$ .