Class 9: Perimeters and Area of Plane Figures – Lecture Notes – ICSE / ISC / CBSE Mathematics Portal for K12 Students

Perimeter and Area of Plane Figures

Triangle Let $a, b, c$ denotes the sides of the Triangle. Then: 1. Perimeter $= a + b + c$ 2. Semi-Perimeter $(s) =$ $\frac{1}{2}$ $(a + b + c)$ 3. Area $= \sqrt{s(s-a)(s-b)(s-c)}$ 4. Area $=$ $\frac{1}{2}$ $\times Base \times Height =$ $\frac{1}{2}$ $bh$
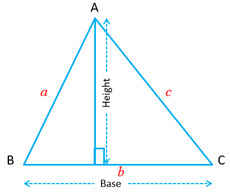Right-angled Triangle Let $b$ be the base, $h$ be the height (or perpendicular) and $a$ be the Hypotenuse. Then, 1. Perimeter $= a + b + h$ 2. Area $=$ $\frac{1}{2}$ $\times Base \times Height =$ $\frac{1}{2}$ $bh$ 3. Hypotenuse $= \sqrt{b^2 + h^2}$
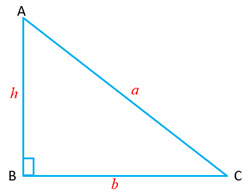Isosceles Right – angled triangle Let the equal sides be $a$ . 1. Hypotenuse $= \sqrt{a^2+a^2} = \sqrt{2} a$ 2. Perimeter $= 2a + \sqrt{2}a$ 3. Area $=$ $\frac{1}{2}$ $\times Base \times Height =$ $\frac{1}{2}$ $a^2$
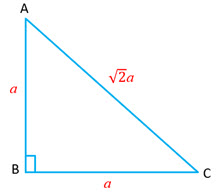Equilateral Triangle Let each of the side is $a$ . Then 1. Perimeter $= 3a$ 2. Height $=$ $\frac{\sqrt{3}}{2}$ $a$ 3. Area $=$ $\frac{1}{2}$ $\times Base \times Height =$ $\frac{1}{2}$ $a \times$ $\frac{\sqrt{3}}{2}$ $a =$ $\frac{\sqrt{3}}{4}$ $a^2$
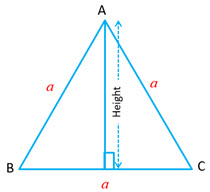Isosceles Triangle Let the equal sides be $a$ . Let the base be $2b$ . Then 1. Perimeter $= 2a+ 2b$ 2. Height $= \sqrt{a^2 - b^2}$ 3. Area $=$ $\frac{1}{2}$ $\times 2b \times \sqrt{a^2 - b^2} = b \sqrt{a^2 - b^2}$
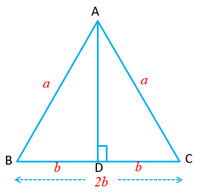Rectangle Let the length $= l$ and breadth $= b$ . Then 1. Perimeter $= 2 (l+b)$ 2. Area $= lb$ 3. Diagonal $= \sqrt{l^2 + b^2}$
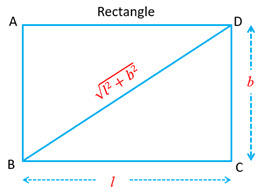Square Let the side of the square $= a$ . Then 1. Perimeter $= 4a$ 2. Area $= a^2$ 3. Diagonal $= \sqrt{2} a$
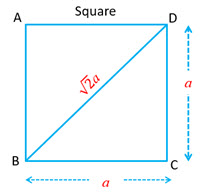Parallelogram Let the two adjacent sides of the parallelogram be $a$ and $b$ 1. Perimeter $= 2 (a+b)$ 2. Area $= Base \times Height$
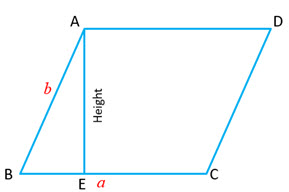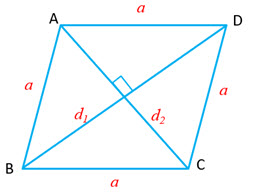
Rhombus A parallelogram that has all the sides equal is called a rhombus. If $d_1$ and $d_2$ are the diagonals, then 1. Side $=$ $\frac{1}{2}$ $\sqrt{{d_1}^2 + {d_2}^2}$ 2. Perimeter $= 4 \times Side = 2\sqrt{{d_1}^2 + {d_2}^2}$ 3. Area $=$ $\frac{1}{2}$ $d_1 d_2$
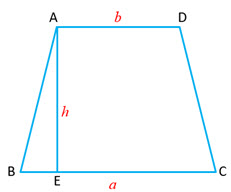
Trapezium A trapezium is a quadrilateral two of whose sides are parallel. A trapezium whose non-parallel sides are equal is known as an isosceles trapezium. Let $a$ and $b$ be the parallel sides and $h$ be the distance between the parallel sides. Then 1. Area $=$ $\frac{1}{2}$ $(a+b) \times h$
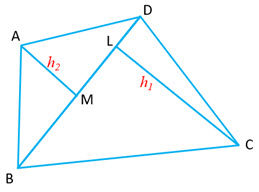
Quadrilateral If $h_1$ and $h_2$ are the perpendicular distances from the diagonal $AC$ of the quadrilateral $ABCD$ from the vertices $B$ and $D$ respectively. Then, 1. Area $=$ $\frac{1}{2}$ $(AC)(h_1 + h_2)$