Class 9: Co-ordinate Geometry – Exercise 19.2

Question 1: Draw the graph of each of the following linear equations:

(i)      (i)      (iii)      (iv)      (v)

(vi)      (vii)      (viii)      (ix)      (x)

(xi)      (xii)      (xiii)      (xiv)

(xv)      (xvi)      (xvii)

(xviii)      (xix)      (xx)

Answer:

i) to viii)

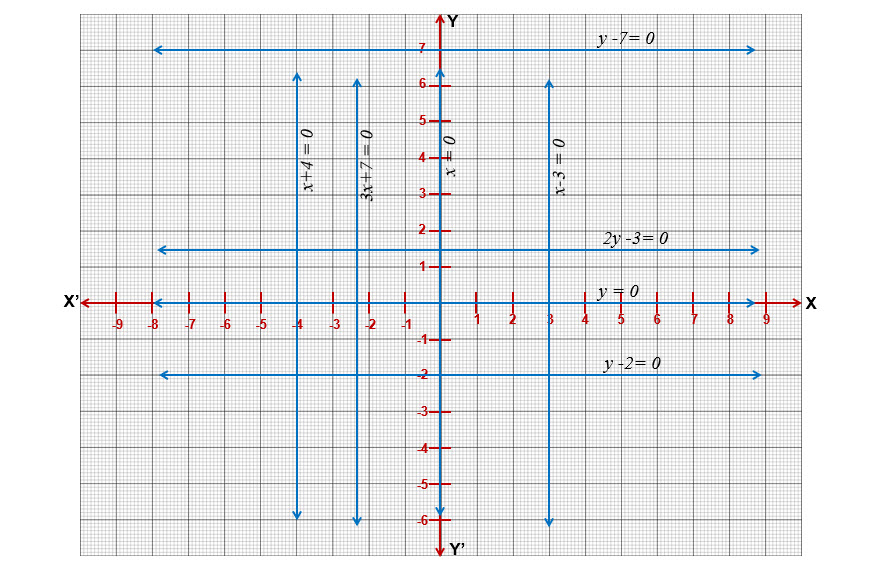
ix) to xii)

xiii) to xvi)

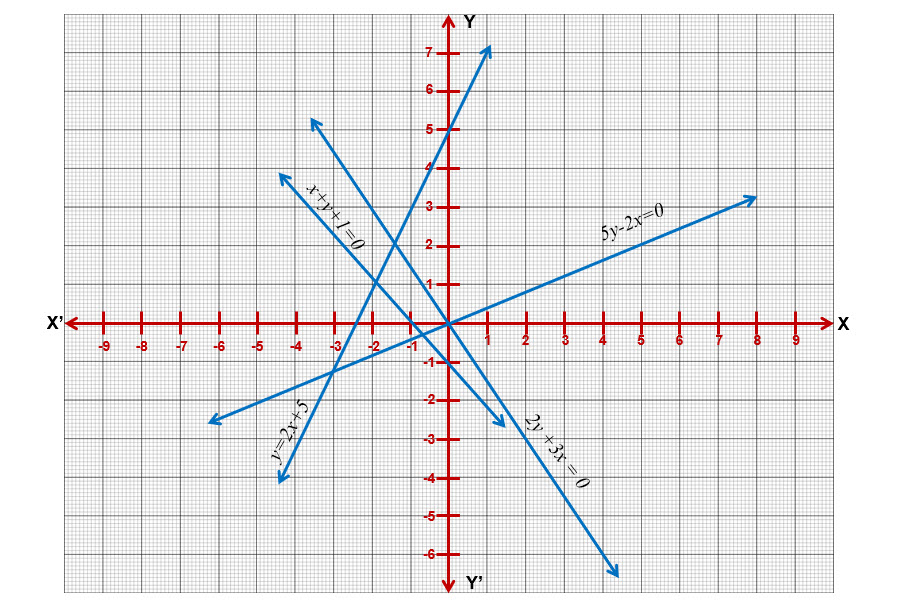
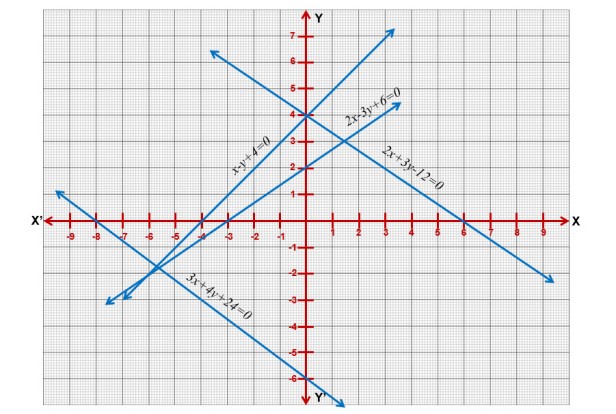
xvii) to xx)

Question 2: Find the slope and y-intercept of the lines represented by each of the following equations:     (i)     (ii)               (iii)    (iv)     (v)

Answer:

For finding the slope and y-intercept, convert the equation into the form

i)

  and 

(ii)

  and 

(iii)

  and 

(iv)

  and 

(v) $

  and 

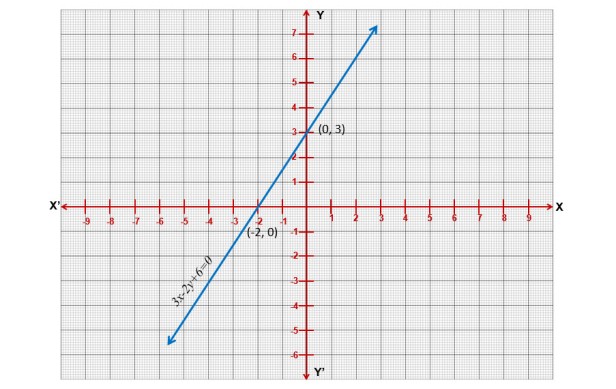
Question 3: Draw the graph of the line represented by the equation . Also, find the coordinates of the points where the line meets with the coordinate axes.

Answer:

To draw the line

x	0	-2
y	3	0

Question 4: Draw the graphs of the lines represented by each of the following equations:     ,        Find the coordinates of the vertices  of the triangle formed by the two lines and the y-axis.

Answer:

To draw the line $latex

x	0	6
y	4	0

To draw the line $latex

x	0	1
y	-1	0

Vertices of the triangle are

Question 5: Draw the graphs of the following pairs of lines on the same graph paper and find their points of intersection. Are these lines perpendicular to each other?     (i) ,                         (ii) ,  

Answer:

i)

To draw the line

x	0	-4
y	4	0

To draw the line

x	0	6
y	6	0

Intersection is . They are perpendicular (from the graph we can see that). Also the slope of the first line is while the slope of the second line is . We know if the product of the two slopes is (which is the case here) the lines are perpendicular.

ii)

To draw the line

x	0	6
y	3	0

To draw the line

x	0	4
y	8	0

Intersection is . They are perpendicular (from the graph we can see that). Also the slope of the first line is while the slope of the second line is . We know if the product of the two slopes is (which is the case here) the lines are perpendicular.

Question 6: Draw the graph of the following pairs of lines on the same graph paper and hence check whether they are parallel or not:

(i) ,       (ii) ,                              (iii) ,    

Answer:

(i) ,  

To draw the line

x	0	-(2/3)
y	2	0

To draw the line

x	0	(4/3)
y	-4	0

 

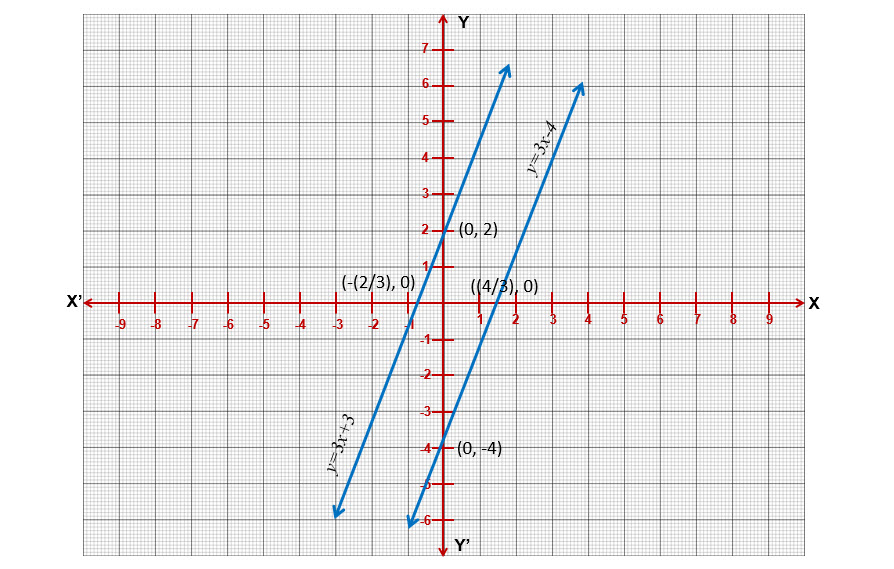
The lines on the graph are parallel. Slope of first line is while the slow of the second line is also . This also proves that the lines are parallel as the slopes of the lines are equal.

(ii) ,    

To draw the line

x	0	2.5
y	5	0

To draw the line

x	0	-7
y	3.5	0

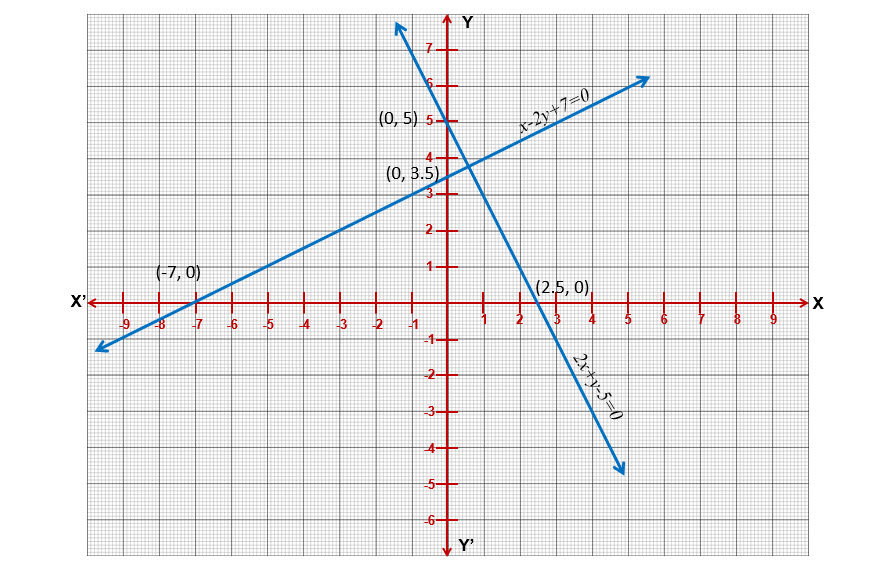
The lines on the graph are not parallel. Slope of first line is while the slow of the second line is also . This also proves that the lines are parallel as the slopes of the lines are not equal.

(iii) ,    

To draw the line

x	0	(8/3)
y	4	0

To draw the line

x	0	-4
y	-6	0

The lines on the graph are parallel. Slope of first line is while the slow of the second line is also . This also proves that the lines are parallel as the slopes of the lines are equal.