Note: If the end points of the diameter is and
, then the equation of the circle is given by:
Question 1: Find the equation of the circle, the end points of whose diameter are and
; Find its center and radius.
Answer:
Given the end points of the diameter as .
Therefore the equation of circle is :
Question 2: Find the equation of the circle the end points of whose diameter are the centers of the circles and
.
Answer:
Given equation of the circle 1:
Given equation of the circle 2:
Therefore the equation of the required circle is:
Question 3: The sides of a square are md
. Find the equation of a circle drawn on the diagonal of the square as its diameter.
Answer:
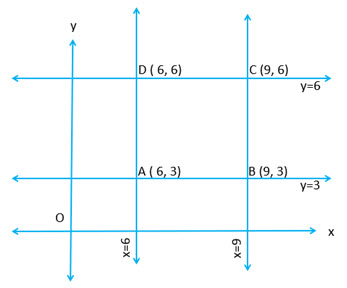 Refer to the adjoining figure.
Refer to the adjoining figure.
The coordinates are
Therefore the equation of the circle is with as the diameter is:
Therefore the equation of the circle is with as the diameter is:
These are the same circle also as you can see from the equations.
Question 4: Find the equation of the circle circumscribing the rectangle whose sides are and
.
Answer:
Given equations:
… … … … … i)
… … … … … ii)
… … … … … iii)
… … … … … iv)
Solving i) & ii) , ii) & iii), iii) & iv) and iv) & i) we get
Therefore the equation of the circle is with as the diameter is:
Therefore the equation of the circle is with as the diameter is:
These are the same circle also as you can see from the equations.
Question 5: Find the equation of the circle passing through the origin and the points where the line meets the axes of coordinates.
Answer:
Given line .
The intercepts on the axes are
Since the circle passes through origin, A and B, we can say that AB is the diameter of the required circle.
Therefore the equation of the circle is with as the diameter is:
Question 6: Find the equation of the circle which passes through the origin and cuts off intercepts and
respectively from x and y-axes.
Answer:
Case 1: Given that the circle passes through and
.
Therefore the equation of the circle is with as the diameter is:
Case 1: Given that the circle passes through and
.
Therefore the equation of the circle is with as the diameter is:
Question 7: Find the equation of the circle whose diameter is the line segment joining and
. Find also the intercept made by it on y-axis.
Answer:
Given the end points of the diameter as .
Therefore the equation of circle is :
… … … … … i)
To find y intercepts, put in i)
Therefore
Therefore the intercept points are
Hence the intercept between the y-axis is
units
Question 8: The abscissae of the two points and
are the roots of the equation
and their ordinates are the roots of the equation
. Find the equation of the circle with
as diameter. Also, find its radius.
Answer:
Roots of equation are
Roots of equation are
Therefore the coordinates of A and B are and
Therefore the equation of the circle is:
Radius
Question 9: is a square whose side is
; taking
and
as axes, prove that the equation of the circle circumscribing the square is
.
Answer:
Since and Ad are x-axis and y-axis respectively, the coordinates are
Since is a diameter, therefore equation of circle is:
Also is a diameter, therefore equation of circle is:
Both are the same circles.
Question 10: The line meets the circle
at
and
. Find the equation of the circle on
as diameter.
Answer:
Given equations:
… … … … … i)
… … … … … ii)
Solving i) and ii) simultaneously,
Therefore equation of the circle is:
Question 11: Find the equation of the circle which circumscribes the triangle formed by the lines and
.
Answer:
Given equations:
… … … … … i)
… … … … … ii)
… … … … … iii)
Solving i), ii) and iii) we get the vertices as
Therefore the equation of the circle with as the diameter is:
Question 12: Find the equations of the circles which pass through the origin and cut off equal chords of units from the lines
and
.
Answer:
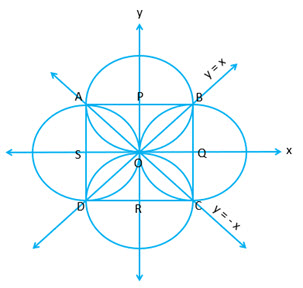 Refer to the adjoining figure.
Refer to the adjoining figure.
Angle between and
is
Therefore angle between and
is
Hence and
are diameters of the circles.
Therefore Radius of circle is
Therefore the coordinates of the vertices of are
Therefore the equation of the circle with as the diameter is:
Therefore the equation of the circle with as the diameter is:
Therefore the equation of the circle with as the diameter is:
Therefore the equation of the circle with as the diameter is:
