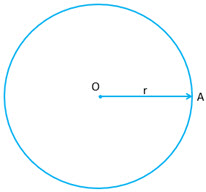a) If r is the radius of a circle then:2019-01-06_8-46-49

  • Perimeter = 2 \pi r
  • Area = \pi r^2   or  Area = \frac{1}{4} \pi d^2
  • Diameter (d) = 2r

 

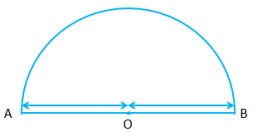b) If r is the radius of a circle then:2019-01-06_8-47-13

  • Perimeter of a semi circle = \pi r + 2r = (\pi + 2)r
  • Area of semi circle = \frac{1}{2} \pi r^2

 

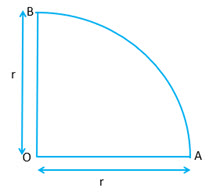c) If r is the radius of a circle then:2019-01-06_8-53-21

  • Perimeter of the quadrant = \frac{1}{4} \times 2 \pi r + 2 r = ( \frac{\pi}{2} + 2)r
  • Area of the quadrant = \frac{1}{4} \pi r^2

 

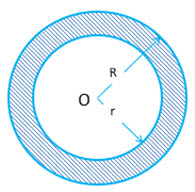d) If R and r are radii of two concentric circles, then2019-01-06_8-52-59

  • Area enclosed between the two circle = \pi R^2 - \pi r^2 = \pi (R^2 - r^2) = \pi (R+r)(R-r)

 

 

 

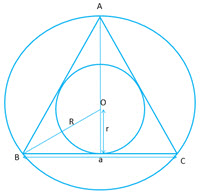2019-01-06_9-12-44e) If  \triangle ABC is an equilateral triangle of side a and height h , then h = \frac{\sqrt{3}}{2} a .

Also if R and r are the radii of the circumscribed and inscribed circles of \triangle ABC , then R = \frac{2h}{3} and r= \frac{h}{3}

  • Circumference of the circumcircle of  \triangle ABC = 2\pi R = = 2 \pi \times \frac{2h}{3} = \frac{4}{3} \pi h
  • Area of the circumcircle = \pi R^2 = \pi ( \frac{2h}{3} )^2 = \frac{4}{9} \pi h^2
  • Circumference of the inscribed circle = 2 \pi r = \frac{2 \pi}{3} h
  • Area of the inscribed circle = \pi r^2 = \frac{1}{9} \pi h^2

f) Important notes:

  • If two circles touch internally, then the distance between their centers is equal to the difference of their radii.
  • If tow circles touch externally. Then the distance between their centers is equal to the sum of their radii.
  • The distance moved by a rotating wheel in one revolution is equal to the circumference of the wheel.
  • The number of revolutions completed by a rotating wheel in one minute = \frac{Distance \ moved \ in \ one \ minute}{circumference}